用双棱镜测钠黄光波长_不确定度

论文导读:：在双棱镜测钠黄光波长实验中，单一的实验方法都有一定的不足或缺陷，为提高实验精度，指明不确定的来源和影响，现将一次成像法和二次成像法相结合，分别对数据处理和不确定度分析进行了比较和说明。之后用二次成像的共轭性对源像距离进行修正，可以提高实验的准确度，实验结果得到了较好好的改进。
论文关键词：双棱镜，一次成像法，二次成像法，虚光源，不确定度
 

1 引言

法国科学家菲涅耳（AugustinJ.Fresnel）在1826年进行的双棱镜实验，证明了光的干涉现象的存在，它不借助光的衍射而形成分波面干涉，用毫米级的测量得到纳米级的精度，其物理思想、实验方法与测量技巧至今仍然值得我们学习。

但是由于实验操作难度大，实验参数的系统误差也较难消除，单一的实验方法都有一定的不足或缺陷不确定度，为提高实验精度，一直是大家探讨的，本文通过常用的一次成像法和二次成像法相结合，对数据进行分析，进行了不确定度的计算。并用共轭性对虚光源（狭缝S）至观察处之距离进行修正，得到良好效果。

2 实验仪器及原理

2.1实验原理和实验仪器

双棱镜干涉实验是波动光学重要实验之一，可用来测光波波长^[1]。干涉原理如图1所示，本实验中是用双棱镜来产生“相干光源”的。

图1 原理图

由双棱镜干涉条件，钠光灯发射的黄色光经单缝而成线光源，光从发出经双棱镜后，形成二虚光源、，该虚光源所发出的光满足干涉条件，在交迭区内产生干涉，成为平行于狭缝的等间距干涉条纹不确定度，由此可得^[2]：

（1）

其中：

：光源之波长。：虚光源、间距，用一次成像法或二次成像法定出。

：干涉条纹的间距，由和决定，可由测微目镜测量求出,根据实际情况选择合适的条纹宽度和条数，本次实验中我们每次测量8条，测量3次龙源期刊。

：虚光源（狭缝S）至观察处之距离，可由光具座标尺读数读出；

2.2虚光源、间距

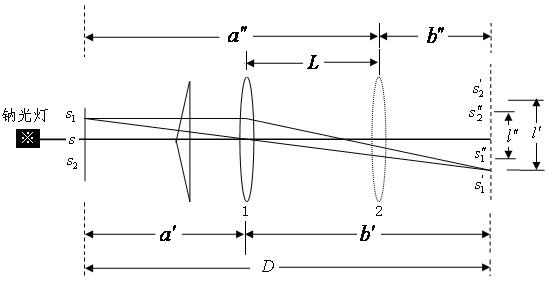
图2 虚光源测量

测量两虚光源间的距离，如图2所示。保持狭缝、双棱镜和测微目镜位置不动，之间放上凸透镜（焦距），调节凸透镜，使其光轴与原各仪器光轴重合。移动透镜，从测微目镜中观察到和的实像，反复改变的位置，使得在中出现清晰的像。记下缝、双棱镜、透镜和测微目镜的位置。

为保证移动透镜时能得到一个放大实像和一个缩小实像不确定度，要求^[3]。其中为两次成像时的间距。

2.2.1一次成像法

一次成像法可以测量曾放大实像和缩小实像两种情况。可以测出、之间的距离，保持和不变，重复测量三次，取平均值。根据透镜成像原理，计算出虚光源的距离。

成大像 （2）

只要求出，值，由就可算出^[2]。

同样道理，根据凸透镜成像的共轭性,移动凸透镜的位置可以找到，第二次成像。

成小像 （3）

其中大像,。

2.2.2二次成像法

也可以由二次成像法^[4]

（4）

3实验数据分析

3.1不确定度的计算及说明

在测量过程中，光具座标尺仪器误差0.5mm，测微目镜仪器误差0.004mm。

直接测量量测量值与其相对不确定度见表1：

表1 直接测量量测量值与其相对不确定度

由公式（1），计算波长的相对不确定公式：

（5）

间接测量量的相对不确定度见表2：

表2 间接测量量的相对不确定度

由公式（5）知道虚光源的不确定度主要取决于光源实像的不确度，而虚光源不确定度将决定测量波长的不确定度。所以，光源实像测量带来的不确定度不确定度，对波长总不确定度的影响最大。下面是一次成像（成放到像）、一次成像（成缩小像）、二次成像法测量的最终表达龙源期刊。

成大像

 1/2    1 2 下一页 尾页