论文导读::采用复变函数的保角映射方法和波函数展开法,根据孔洞与内部流体在界面上的应力和位移连续的边界条件,得到了充满流体的任意形状的孔洞对入射平面P波的散射问题的理论解,以椭圆形孔洞为例,着重分析了椭圆的长短轴之比、流体的存在与否以及入射频率对散射幅值的影响,结果表明:(1) 圆形孔洞的分波波谱的峰值分布均匀,而椭圆形孔洞则不均匀;(2) 散射P波的波谱主要集中于前进方向和背向一侧,而散射S波的波谱主要集中于与传播方向垂直的一侧;(3) 入射波与孔洞的作用面积越大,散射P波的波谱也越大,而散射S波的波谱也越小;(4) 当孔洞为圆形时,流体对散射P波和S波的波谱影响最小,即此时流体与孔壁的动力相互作用最小。
论文关键词:平面P波,任意形状的孔洞,流体,分波波谱,散射幅值
0引言
波在无限的均匀介质里,是以常速度沿着固定路线不受干扰地向前传播的,但若有障碍物嵌入,则会发生散射[1]。散射波的散射信息中包含散射体自身的一些特征信息,根据弹性波在孔洞的散射特性可以进行坝体管涌、岩体超前预报、路面脱空等无损检测和地震勘测,近年来已引起广泛的重视。由于弹性波在界面会产生耦合散射,因此弹性波的散射比声波、电磁波要复杂得多。
自上世纪五十年代以来,国内外众多学者基于波函数展开法已对圆形孔洞对P波和SV波的散射,基于保角变换对椭圆形等不规则形状的孔洞对SH波的散射等问题进行了研究,理论已经很成熟[2-7]论文格式范文。但是关于不规则形状的孔洞(特别是充满其它介质例如流体)对P波散射的研究不多。
本文采用保角变换和波函数展开法,得到平面P波在充满流体的任意形状孔洞的散射问题的理论解,以椭圆形孔洞为实例分波波谱,着重讨论了流体的存在与否、以及椭圆的长短轴之比以及入射频率对散射幅值的影响。
1波场的势函数展开
1.1 入射P波的势函数
取 为入射P波的幅值,则在直角坐标系( 为入射P波的幅值,则在直角坐标系( )下,入射P波可以表示为 )下,入射P波可以表示为
 (1) (1)
式中,上标inc表示入射; 为入射P波与x轴的夹角; 为入射P波与x轴的夹角; 为周围介质中P波的波数;为了研究和讨论方便,式(1)及以下的公式中都略去了公共时间因子 为周围介质中P波的波数;为了研究和讨论方便,式(1)及以下的公式中都略去了公共时间因子 。 。
根据复数坐标 ,则式(1)可以写成 ,则式(1)可以写成
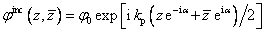 (2) (2)
1.2 散射P波和S波的势函数
入射P波会在孔洞上产生耦合散射,即散射波包含P波和SV波成分,根据关系式 , , ,则满足稳态波动方程及远场幅射Sommerfeld条件的散射P波和SV波的势函数可表示成 ,则满足稳态波动方程及远场幅射Sommerfeld条件的散射P波和SV波的势函数可表示成
 (3a) (3a)
 (3b) (3b)
式中,上标sc表示散射; 和 和 为待定复系数; 为待定复系数; 为n阶第一类Hankel函数; 为n阶第一类Hankel函数; 为周围介质SV波的波数。 为周围介质SV波的波数。
1.3 流体中折射P波的势函数
由于流体中的剪切模量 ,所以不存在S波,只存在P波,参考文献[3],在复平面下,流体折射P波的势函数为 ,所以不存在S波,只存在P波,参考文献[3],在复平面下,流体折射P波的势函数为
 (4) (4)
式中,上标re表示折射; 为待定复系数; 为待定复系数; 为n阶第一类Bessel函数; 为n阶第一类Bessel函数; 为孔洞中充填流体的P波波数。 为孔洞中充填流体的P波波数。
引入保角变换 ,则波场势函数式(2)~(4)可表示成极坐标系( ,则波场势函数式(2)~(4)可表示成极坐标系( )下的形式 )下的形式

(5a)
 (5b) (5b)
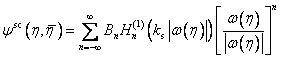 (5c) (5c)
 (5d) (5d)
式中, ~ ~ 为待定复系数。 为待定复系数。
2问题的求解
根据弹性力学,极坐标系( )下应力正应力 )下应力正应力 、剪应力 、剪应力 和径向位移 和径向位移 可根据相关公式由势函数展开式求得[8] 可根据相关公式由势函数展开式求得[8]

 (6a) (6a)
 (6b) (6b)
 (6c) (6c)
式中, 和 和 为Lamé弹性常量。 为Lamé弹性常量。
将任意形状的孔洞进行保角变换为单位圆 ,假定周围介质是不透水的,则界面处( ,假定周围介质是不透水的,则界面处( )周围介质与流体满足 )周围介质与流体满足
 ; ; ; ; (7) (7)
联立式(5)~(7),经过整理可得关于待定复系数 ~ ~ 的方程组 的方程组
 (i=1~3) (8) (i=1~3) (8)
式中分波波谱,取 , , , , ,其它各元素的详细表达式如下: ,其它各元素的详细表达式如下:
 ; ;
 ; ;
 ; ;
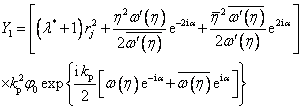 ; ;
 ; ;
1/2 1 2 下一页 尾页 |


