 为逻辑函数,用来判别接触与否。(5) 为逻辑函数,用来判别接触与否。(5)
3 系统刚柔耦合碰撞动力学方程
3.1 系统动能
如图2,在浮动系中,对于未变形时梁上一点P(x,0),其变形后的位置矢量为
 (6) (6)
则该点的速度为
 (7) (7)
系统的动能为
 (8) (8)
3.2 系统势能
系统势能包括柔性梁的弹性势能,重力势能,以及作为有势力处理的碰撞力产生的碰撞力势能。这里我们引入碰撞力势能概念,其目的是便于计算碰撞力所对应的广义力。整个系统的势能为
 (9) (9)
柔性梁的弹性变形势能即为梁的横向弯曲势能为
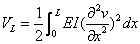 (10) (10)
梁的重力势能为
  (11) (11)
式(11)中的 是重力加速度矢量在惯性系中坐标列阵, 是重力加速度矢量在惯性系中坐标列阵, 是质量微元的位置矢量在浮动系中坐标列阵。 是质量微元的位置矢量在浮动系中坐标列阵。
在每一个积分步内,因步长很短,碰撞力可以作为有势力处理,碰撞力势能形式如下
 (12) (12)
式(12)中 为惯性系中碰撞力方向矢量列阵, 为惯性系中碰撞力方向矢量列阵, 是碰撞力大小, 是碰撞力大小, 为惯性系到浮动系的齐次变换矩阵(在本问题中可以简化为方向余弦阵)物理论文, 为惯性系到浮动系的齐次变换矩阵(在本问题中可以简化为方向余弦阵)物理论文, 为浮动系中碰撞力作用点位置矢量列阵。碰撞力势能只在碰撞发生过程中起作用,其余时间碰撞力势能为0。 为浮动系中碰撞力作用点位置矢量列阵。碰撞力势能只在碰撞发生过程中起作用,其余时间碰撞力势能为0。
3.3 假设模态法离散
本文采用假设模态法对柔性梁的横向变形位移进行离散,即
 (13) (13)
式(13)中的 为梁的横向模态函数, 为梁的横向模态函数, 为模态坐标, 为模态坐标, 为模态截断数。 为模态截断数。
式(1)表示的非线性耦合变形项又可表示为
 (14) (14)
其中
 (15) (15)
3.4 系统刚柔耦合碰撞动力学方程
取广义坐标 ,运用第二类拉格朗日方程 ,运用第二类拉格朗日方程
 (16) (16)
其中 为除去重力和碰撞力后剩下的外主动力产生的广义力列阵,可表示为 为除去重力和碰撞力后剩下的外主动力产生的广义力列阵,可表示为
 (17) (17)
式(17)中的 是如图1中的作用在转轴处的驱动力矩。 是如图1中的作用在转轴处的驱动力矩。
将所求得的动能和势能代入式(16),经过推导得到可以计及碰撞过程的系统全局刚柔耦合动力学方程
 (18) (18)
其中 为广义质量阵, 为广义质量阵, 为广义力列阵。 为广义力列阵。
 (19) (19)
 (20) (20)
 为无碰撞时广义力列阵。(21) 为无碰撞时广义力列阵。(21)
 为碰撞广义力列阵,在无碰撞时为0。(22) 为碰撞广义力列阵,在无碰撞时为0。(22)
式中:
 (23) (23)
 (24) (24)
 (25) (25)
 (26) (26)
 (27) (27)
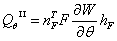 (28) (28)
 (29) (29)
在广义质量阵和广义力阵的元素中, 、 、 、 、 、 、 、 、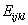 、 、 为与时间无关的常数。 为与时间无关的常数。
由于建模时在变形位移中考虑了二次耦合变形量,因此在推导出的刚柔耦合动力学方程中,比传统的零次耦合动力学方程增加了附加耦合项(上述式子中的带下划线的项),这些附加的耦合项出现在广义质量阵和广义力阵中,传统的动力学模型中不包含下划线项。加入下划线项后,广义质量阵右下角矩阵不再是常数阵,而是广义坐标的非线性阵,惯量高度耦合。在式(27)中的下划线项加入后,会增加刚度项,以及阻尼项,尤其是与转动有关的刚度项整体将会由原来的负变成正,即下划线项产生动力刚化效应,且比柔化效应大,从而整体是动力刚化,且随转速增加而增加。在低转速时,无论刚化还是柔化效应跟结构的静刚度比显得度很小,但当高转速时,大位移运动产生的这种效应就会增加,此时两种不同模型的差异就明显增大,到临界转速时产生本质差别。
碰撞力产生的效应体现在式(28)和(29)上。虽然其结构和式(26)和(27)的最后项对应相同,都代表的是系统外主动力效应,但由于其作用特点不同,产生与通常外主动力很不相同的效应。由于碰撞力作用强度大且变化剧烈,它就能迅速激发高频,而高频的加入使得方程不稳定,求解速度明显下降。从数学上看,增加了原来问题的多尺度性和非连续性,问题变得异常复杂,对方程求解提出了更高的要求。
4 碰撞动力学仿真结果
对图1所示的系统取如下的结构参数: =2.6×103㎏/m3,E=71.96GPa,L=0.7112m,I=1.24×10-10m4,b=0.0163m,h=0.0045m,R=0.01m。 =2.6×103㎏/m3,E=71.96GPa,L=0.7112m,I=1.24×10-10m4,b=0.0163m,h=0.0045m,R=0.01m。
4.1 刚柔耦合模型与传统零次耦合模型的结果对比
为了对比刚柔耦合模型(也称一次耦合模型)与传统零次耦合模型的区别与联系,进行了不同大范围运动下的系统动力学响应计算。选取不同大小的初始角速度,在不含碰撞的重力场中系统作大范围运动情况下,对两种模型分别进行动力学仿真物理论文,并将计算出的梁末端横向变形位移进行对比。仿真中,低速情况取初始角速度为5rad/s,高速情况取初始角速度为100rad/s。
图3和图4分别是大范围运动为低速和高速情况下的梁末端横向变形响应。由图可见,在大范围运动为低速时,刚柔耦合模型与零次耦合模型的计算结果非常接近;在大范围运动为高速时,刚柔耦合模型的梁末端变形依旧保持周期性变化,而零次耦合模型的梁末端变形量持续增大,趋向于发散,这与实际物理现象不符。仿真结果说明,在大范围运动为较低速度时,刚柔耦合模型与零次耦合模型的计算结果差别不大,这也验证了刚柔耦合模型的准确性;在大范围运动为较高速度时,传统的零次耦合模型已经不再适用,而刚柔耦合模型仍可较好的反映系统的动力学特性论文格式范文。
2/3 首页 上一页 1 2 3 下一页 尾页 |


