论文摘要:约束优化问题是生产实际中的常见问题,本文列举了常用约束优化问题的几种算法,同时对它们的特点进行了总结,并通过MATLAB软件对算法进行实现。
关键词:最优化 约束 算法
[1 数学模型]
一般的约束最优化问题,其数学模型为

 (1) (1)
的约束优化问题,就是要在可行域

中,找到一个可行点 ,使目标函数 ,使目标函数 取得最小值。此时称 取得最小值。此时称 为问题(1)的最优解。 为问题(1)的最优解。
[2 常用约束优化算法简介]
[2.1 外点罚函数法]
基本思想:对违反约束条件的点在目标函数中加入相应的“惩罚”,而对可行域内的点不予惩罚。其迭代点一般在可行域外部移动,随着一个无约束问题的求解转移到另一个无约束问题的求解,惩罚次数逐渐加大,从而迫使迭代点向可行域靠近。具体过程如下:
对问题(1),构造一个函数为

其中惩罚函数 为 为
 (2) (2)
 
 是一个逐渐增大的参数,称为惩罚因子。 是一个逐渐增大的参数,称为惩罚因子。 称为问题(1)的增广目标函数。 称为问题(1)的增广目标函数。
显然, 是定义在 是定义在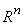 上的一个无约束函数,关于市场营销的论文由增广目标函数 上的一个无约束函数,关于市场营销的论文由增广目标函数 的构造可知,如果已经求出 的构造可知,如果已经求出 的最优解为 的最优解为 ,则判断 ,则判断 是否属于 是否属于 。 。
(1) 如果 ,则 ,则 是问题(1)的最优解; 是问题(1)的最优解;
(2) 如果 ,则 ,则 不是问题(1)的最优解。此时说明原来的罚因子给小了,需要加大罚因子,使得 不是问题(1)的最优解。此时说明原来的罚因子给小了,需要加大罚因子,使得 ,然后再重新计算 ,然后再重新计算 的最优解。 的最优解。
事实上,随着罚因子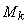 的增大,迫使惩罚项的值逐渐减小,从而使 的增大,迫使惩罚项的值逐渐减小,从而使 的极小点 的极小点 沿着某一轨迹逐渐接近于可行域 沿着某一轨迹逐渐接近于可行域 上的最优点 上的最优点 。当 。当 趋于无穷大时, 趋于无穷大时, 的极小点就是原问题(1)的最优点 的极小点就是原问题(1)的最优点 。 。
算法特点:外点罚函数法的优点是在整个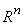 空间进行优化,因此对于初始点的要求不高,可以任意选取;对于等式约束,不等式约束或者两者都包含的混合约束均可应用,从而使外点罚函数法较广泛地应用到求解各种形式的约束优化问题中。缺点是 空间进行优化,因此对于初始点的要求不高,可以任意选取;对于等式约束,不等式约束或者两者都包含的混合约束均可应用,从而使外点罚函数法较广泛地应用到求解各种形式的约束优化问题中。缺点是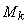 的选取并非是越大越好,如果 的选取并非是越大越好,如果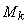 取得过大,初始解就会越接近可行域,似乎求解一次无约束优化问题就可以找到约束问题的最优解,减少迭代次数,但是,当 取得过大,初始解就会越接近可行域,似乎求解一次无约束优化问题就可以找到约束问题的最优解,减少迭代次数,但是,当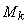 越大,增广目标函数 越大,增广目标函数 的Hesse矩阵的条件越坏,使Hesse矩阵可能陷入病态,对搜索产生较大的困难;如果 的Hesse矩阵的条件越坏,使Hesse矩阵可能陷入病态,对搜索产生较大的困难;如果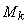 取得过小,则罚函数的极小点远离约束问题的最优解,则会增加计算量,使计算效率很低。外点罚函数法的中间结果不是可行解,不能作为近似最优解,只有迭代到最后才能得到符合要求的可行解。 取得过小,则罚函数的极小点远离约束问题的最优解,则会增加计算量,使计算效率很低。外点罚函数法的中间结果不是可行解,不能作为近似最优解,只有迭代到最后才能得到符合要求的可行解。
1/4 1 2 3 4 下一页 尾页 |


