论文导读::因此我们通过使用双因素方差分析来对数据进行分析。在测量半导体材料的霍尔效应实验和霍尔元件测量[1]中。这个电势差就是霍尔电压。
论文关键词:双因素方差分析,霍尔效应,霍尔电压
一.引言
在测量半导体材料的霍尔效应实验和霍尔元件测量[1]中,我们经常需要判断不同的温度和不同的磁场强度对霍尔电压这一指标有无显著影响,以选取合适条件。为此,我们在不同温度和不同磁场强度下做实验,在某一段温度范围和某一段磁场范围内,实验数据总是呈现波动状态。引起波动的原因可以分为两类:一类是由实验条件不同引起的,这是可以控制的因素,因此由实验条件引起的波动是系统波动;另一类是由随机因素引起的,这是不可控制的因素,因此由随机因素引起的波动是偶然波动。这两类波动总是混杂在一起,使实验数据呈现总的波动状态。我们的目的是要对实验数据进行分析,把总的波动分为两部分:一部分是由实验条件引起的系统波动,另一部分是由随机因素引起的偶然波动,并对这俩部分加以比较,判断不同的实验条件对实验结果是否有显著影响。因此我们通过使用双因素方差分析来对数据进行分析。
二.霍尔效应[2]
如图1所示,样品通以电流I,如果在垂直于样品表面且与电流垂直的方向上加一磁场,如图所示样品就会产生一个与电流和磁场方向垂直的电势差,这个电势差就是霍尔电压


图1
 与样品厚度d成反比,与磁感应强度 与样品厚度d成反比,与磁感应强度 和电流I成正比霍尔电压,比例系数 和电流I成正比霍尔电压,比例系数 叫做霍尔系数。 叫做霍尔系数。
霍尔电势差是这样产生的:当电流通过样品(假设为P型半导体)时,空穴有一定的漂移速度

式中q为电子电荷。洛伦兹力使电荷产生横向偏转,由于样品存在边界,所以有些偏移的载流子将在边界积累起来,形成一个横向电场E,直到电场对载流子的作用力 与磁场作用的洛伦兹力相抵消为止,即 与磁场作用的洛伦兹力相抵消为止,即

这时电荷在样品中流动将不再发生偏转,霍尔电势差 就是由这个电场建立起来的。如果样品是n型半导体,则横向电场与前者相反中国期刊全文数据库。 就是由这个电场建立起来的。如果样品是n型半导体,则横向电场与前者相反中国期刊全文数据库。
三.双因素方差分析模型的建立[3][4]
|
|
场强因素B
|
平均值
|
|
  …… ……
|
|
温
度
因
素
T
|




|
  …… ……
  …… ……
  
  …… ……
|




|
|
平均值
|
  …… ……
|

|
| |
|
|
|
表1
表1中,设温度因素T有 个不同的水平 个不同的水平 , , ,…… ,…… ,因素B有 ,因素B有 个不同的水平 个不同的水平 , , ,…… ,……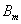 ,共有 ,共有 个不同的水平组合( 个不同的水平组合( , , )( )(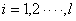 , , )共得到 )共得到 个结果 个结果 。 。
上述假设可用下面的数据结构表示:
  , , (1) (1)
其中 为水平组合为( 为水平组合为( , , )下的实验结果, )下的实验结果, 是水平组合为( 是水平组合为( , , )时总体的数学期望, )时总体的数学期望, 为相应的实验误差,它是由实验中不可控制的各种偶然因素引起的随机波动。引入 为相应的实验误差,它是由实验中不可控制的各种偶然因素引起的随机波动。引入
 , ,
 , ,

记
 , ,
 , ,
称 为总平均, 为总平均, 为温度因素T的第 为温度因素T的第 水平 水平 的效应, 的效应, 为场强因素B的第 为场强因素B的第 水平 水平 的效应,它们分别反映水平 的效应,它们分别反映水平 和 和 对实验指标的作用。我们假定T,B两因素之间不存在交互作用,故可假定 对实验指标的作用。我们假定T,B两因素之间不存在交互作用,故可假定

即水平组合( , , )的联合影响等于它们各自影响的叠加。于是(1)式可改写为 )的联合影响等于它们各自影响的叠加。于是(1)式可改写为

 , , (2) (2)
1/2 1 2 下一页 尾页 |


