 (15) (15)
其中:
  ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ;
 ; ; ; ; ; ; 
 ; ;

   、 、 、 、 同前所述. (16) 同前所述. (16)
1.3 GER格式
当 为奇数时,在右边界上的每两个内点 为奇数时,在右边界上的每两个内点 、 、 (其中: (其中: )组成一组,采用式(2)中的第一式和第三式;在上边界上的每两个内点 )组成一组,采用式(2)中的第一式和第三式;在上边界上的每两个内点 、 、 (其中: (其中: )组成一组,采用式(2)中的第一式和第二式;在 )组成一组,采用式(2)中的第一式和第二式;在 点采用式(2)中的第一式;在其余 点采用式(2)中的第一式;在其余 个节点处反复使用GE格式(2),就得GER格式,其矩阵形式为: 个节点处反复使用GE格式(2),就得GER格式,其矩阵形式为:
 (17) (17)
其中:
  ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ;    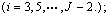
 
 ; ; ; ; ; ; ; ; ; ; ; ; 同前所述. (18) 同前所述. (18)
由(9)—(12)式可得:
定理1 当 且 且 时,式(13) 、式(15) 、式(17)的精度一般为 时,式(13) 、式(15) 、式(17)的精度一般为 . .
2 稳定性分析
我们首先对GE格式的稳定性进行分析,由式(13)的增长矩阵的特征方程可得:
 (19) (19)
则: (20) (20)
从而: (21) (21)
其中: ( ( 为特征值) (22) 为特征值) (22)
因 是一个下三角行列式,故显然有: 是一个下三角行列式,故显然有:
 且 且
解得:
又当 时, 时,  , ,
从而:

递推可知: 对 对 有界. 有界.
从而可得:
定理2 GE格式(13)的稳定性条件为
类似可得:
定理3 当取 时,GEL格式(15)、GER格式(17)是稳定的. 时,GEL格式(15)、GER格式(17)是稳定的.
3 数值例子
考虑二维双曲型方程初边值问题:
 (23) (23)
它的精确解为: . .
以下数值例子取 对GE格式取 对GE格式取 ,对GEL、GER格式取 ,对GEL、GER格式取 . .
2/3 首页 上一页 1 2 3 下一页 尾页 |


