论文导读::本文构造了求解二维双曲型方程 的初边值问题的一组分组并行算法(GE、GEL、GER),格式的局部截断误差阶一般为 的初边值问题的一组分组并行算法(GE、GEL、GER),格式的局部截断误差阶一般为 ,稳定性条件为 ,稳定性条件为 .数值例子验证了理论结果. .数值例子验证了理论结果.
论文关键词:二维双曲型方程,分组显式格式:稳定性:截断误差
0 引言
设数学模型为:
 (1) (1)
由于对此方程的计算具有极强的方向性且仅具有单边边界条件,故对二维双曲型串行差分格式的并行化是一件很不容易的事情.从已有文献看(见文[1]、[2]、[3]、[4]),尚未发现二维双曲型方程的并行化格式.本文利用一个二维显格式、两个二维显隐格式和一个二维隐格式构造了一组分组显式格式,格式的局部截断误差阶一般为 ,稳定性条件为 ,稳定性条件为 . .
1 构造并行差分格式
设问题(1)的解 充分光滑,以 充分光滑,以 、 、 和 和 分别为 分别为 、 、 和 和 方向的网络步长,其中: 方向的网络步长,其中: , , , , 为正整数,在网点 为正整数,在网点 处的网格函数 处的网格函数 记为 记为 ,其近似值记为 ,其近似值记为 .其中 .其中   为简单起见,本文取 为简单起见,本文取 且 且 ,则 ,则 ,其中 ,其中 . .
下面针对 奇偶性数学建模论文,设计如下几种分组并行的计算方法: 奇偶性数学建模论文,设计如下几种分组并行的计算方法:
1.1 GE格式
当 为偶数时,为了设计分组并行差分格式,用如下的四个格式构造逼近式(1)的并行差分方程组: 为偶数时,为了设计分组并行差分格式,用如下的四个格式构造逼近式(1)的并行差分方程组:
 (2) (2)
其中 于是在第 于是在第 时间层上的4个函数值可由第 时间层上的4个函数值可由第 时间层上的8个函数值显式地进行计算: 时间层上的8个函数值显式地进行计算:
 即: 即:  (7) (7)
其中:
  ; ;
 ; ; (8) (8)
将式(3)、(4)、(5)、(6)分别在 、 、 、 、 、 、 处进行Taylor级数展开(见文[5])得它们的局部截断误差分别为: 处进行Taylor级数展开(见文[5])得它们的局部截断误差分别为:
 (9) (9)
 (10) (10)
 (11) (11)
 (12) (12)
其中: . .
我们可将每一时间层上的节点(除左边界点和下边界点外)按 、 、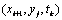 、 、 、 、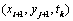 (其中: (其中: )四个相邻点组成一组,共分为 )四个相邻点组成一组,共分为 组.并对每组都使用GE格式(2).且可显式表示为: 组.并对每组都使用GE格式(2).且可显式表示为:
 (13) (13)
其中:

 ; ; ; ; ; ;
 
 
 
   (14) (14)
1.2 GEL格式
当 为奇数时,在靠近下边界的每两个内点 为奇数时,在靠近下边界的每两个内点 、 、 ( ( )组成一组,采用式(2)中的第一式和第二式;在靠近左边界的每两个内点 )组成一组,采用式(2)中的第一式和第二式;在靠近左边界的每两个内点 、 、 ( (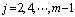 )组成一组,采用式(2)中的第一式和第三式;在 )组成一组,采用式(2)中的第一式和第三式;在 点采用式(2)中的第一式;在其余 点采用式(2)中的第一式;在其余 个节点处反复使用GE格式(2),就得GEL格式,其矩阵形式为: 个节点处反复使用GE格式(2),就得GEL格式,其矩阵形式为:
1/3 1 2 3 下一页 尾页 |


