Z ,Z ,Z 分别是票贩子和售票员、警察合谋时的福利损失,为了获得租金,票贩子对售票员行贿,行贿金额为Y,此时,票贩子获得剩余支付Z-Y。为了逃避警察的查获可能向警察行贿,行贿金额为K,假设票贩子是理性人,票贩子只有与售票员合谋才会发生与警察的合谋行为,票贩子获得剩余支付Z-Y-K。警察检查的成本为M。为了防止寻租行为的发生,监督者会付出相应的检查成本L 分别是票贩子和售票员、警察合谋时的福利损失,为了获得租金,票贩子对售票员行贿,行贿金额为Y,此时,票贩子获得剩余支付Z-Y。为了逃避警察的查获可能向警察行贿,行贿金额为K,假设票贩子是理性人,票贩子只有与售票员合谋才会发生与警察的合谋行为,票贩子获得剩余支付Z-Y-K。警察检查的成本为M。为了防止寻租行为的发生,监督者会付出相应的检查成本L ,L ,L ,如果查出寻租行为将分别对票贩子、售票员和警察处罚H ,如果查出寻租行为将分别对票贩子、售票员和警察处罚H ,H ,H 和H 和H 0,其都为净处罚(扣除非法所得后的处罚)。假设警察检查票贩子和售票员合谋行为的概率为 0,其都为净处罚(扣除非法所得后的处罚)。假设警察检查票贩子和售票员合谋行为的概率为 ,政府检查票贩子与售票员的合谋及与警察的合谋的概率分别为 ,政府检查票贩子与售票员的合谋及与警察的合谋的概率分别为 , , 。票贩子与售票员及警察合谋的概率分别为 。票贩子与售票员及警察合谋的概率分别为 , , ,引入监督者后票贩子与售票员及警察合谋的概率分别为 ,引入监督者后票贩子与售票员及警察合谋的概率分别为 , , 。票贩子坦白其与售票员及警察的合谋行为的概率分别为 。票贩子坦白其与售票员及警察的合谋行为的概率分别为 , , 。票贩子坦白与售票员及警察的合谋后减轻的处罚分别为S 。票贩子坦白与售票员及警察的合谋后减轻的处罚分别为S ,S ,S 。 。
3.1.1警察,售票员,票贩子三方博弈模型的建立与求解
(1)票贩子与售票员、警察合谋,且警察选择不查,则警察、售票员、票贩子的收益分别为K、Y、Z-Y-K。
(2)票贩子与售票员合谋且与警察非合谋的情况下,警察选择不查,则三者的收益分别为0、Y、Z-Y。
(3)票贩子与售票员合谋且与警察非合谋的情况下,且警察选择检查。合谋行为被查出,若票贩子选择隐瞒则三者收益分别为 、 、 、 、 。若票贩子选择坦白则三者收益分别为 。若票贩子选择坦白则三者收益分别为 、 、 、 、 。 。
(4)票贩子与售票员、警察非合谋的情况下,警察选择不查,则三者收益分别为0、0、0,若警察选择检查,则三者收益分别为-M、0、0。
给定票贩子和售票员合谋的概率 警察选择合谋( 警察选择合谋( =1)和非合谋( =1)和非合谋( =0)的期望收益分别为: =0)的期望收益分别为:
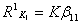
 = =
解 = = ,得 ,得 如果票贩子与售票员合谋的概率小于 如果票贩子与售票员合谋的概率小于 ,警察的最优选择是合谋。如果其合谋概率大于 ,警察的最优选择是合谋。如果其合谋概率大于 ,警察最优选择是合谋,如果其合谋概率等于 ,警察最优选择是合谋,如果其合谋概率等于 ,警察随机选择合谋和不合谋。 ,警察随机选择合谋和不合谋。
给定警察选择检查的概率 ,售票员选择合谋( ,售票员选择合谋( =1)和非合谋( =1)和非合谋( =0)的期望收益分别为: =0)的期望收益分别为:


解 ,得 ,得 如果警察选择检查的概率小于 如果警察选择检查的概率小于 ,售票员的最优选择是合谋。如果其检查概率大于 ,售票员的最优选择是合谋。如果其检查概率大于 ,售票员最优选择是非合谋,如果其检查概率等于 ,售票员最优选择是非合谋,如果其检查概率等于 ,售票员随机选择合谋和不合谋。 ,售票员随机选择合谋和不合谋。
给定警察选择检查的概率 ,票贩子选择与票贩子合谋( ,票贩子选择与票贩子合谋( =1)和非合谋( =1)和非合谋( =0)的期望收益分别为: =0)的期望收益分别为:
 
解 ,得 ,得 如果警察选择检查的概率小于 如果警察选择检查的概率小于 ,票贩子的最优选择是合谋。如果其检查概率大于 ,票贩子的最优选择是合谋。如果其检查概率大于 ,票贩子最优选择是非合谋,如果其检查概率等于 ,票贩子最优选择是非合谋,如果其检查概率等于 ,票贩子随机选择合谋和不合谋。 ,票贩子随机选择合谋和不合谋。
此外,警察选择非合谋情况下,票贩子的收益
 
我们得出此模型的混合战略纳什均衡解:
 , , (1) (1)
 , , (2) (2)
因此,为了打击票贩子寻租行为,警察应当以 最优概率检查售票员是否受贿,应当以 最优概率检查售票员是否受贿,应当以 最优概率检查票贩子是否行贿。 最优概率检查票贩子是否行贿。
3.1.2监督者,售票员,票贩子三方博弈模型的的建立与求解
(1)票贩子与售票员合谋,且监督者选择检查。合谋行为被查出,若票贩子坦白,则监督者、售票员、票贩子的收益为 、 、 、 、 ,若票贩子隐瞒,则三者收益为 ,若票贩子隐瞒,则三者收益为 、 、 、 、 。 。
(2)票贩子与售票员合谋,且监督者选择不查,则三者收益分别为 、 、 、 、 。 。
(3)票贩子与售票员非合谋,若监督者选择检查,则三者收益分别为 、0、0,若监督者选择不查,则三者收益分别为0、0、0. 、0、0,若监督者选择不查,则三者收益分别为0、0、0.
给定票贩子和售票员合谋的概率为 ,监督者选择检查( ,监督者选择检查( =1)和不查( =1)和不查( =0)的期望收益分别为: =0)的期望收益分别为:


解 ,得 ,得 如果票贩子和售票员选择合谋的概率小于 如果票贩子和售票员选择合谋的概率小于 ,监督者的最优选择是不查。如果其合谋概率大于 ,监督者的最优选择是不查。如果其合谋概率大于 ,监督者最优选择是检查,如果其合谋概率等于 ,监督者最优选择是检查,如果其合谋概率等于 ,监督者随机选择检查和不查。 ,监督者随机选择检查和不查。
给定监督者检查的概率 ,售票员选择合谋( ,售票员选择合谋( =1)和非合谋( =1)和非合谋( =0)的期望收益分别为: =0)的期望收益分别为:


解 ,得 ,得 如果监督者检查的概率小于 如果监督者检查的概率小于 ,售票员的最优选择是合谋。如果其检查概率大于 ,售票员的最优选择是合谋。如果其检查概率大于 ,售票员最优选择是不合谋,如果其检查概率等于 ,售票员最优选择是不合谋,如果其检查概率等于 ,售票员随机选择合谋和不合谋。 ,售票员随机选择合谋和不合谋。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


