论文导读:：数学软件的普及，对传统的高等数学教学产生了巨大影响。在极限的教学中引入数学软件Mathematica，通过应用数据显示，绘制图形，动画，数值计算等功能的介绍，使学生对概念的理解以及对极限的学习都得到了很好的改善，也使得课堂教学更具活力。
论文关键词：极限，Mathematica，绘图
随着全国大学生数学建模竞赛的影响日益扩大，数学软件使用越来越普及，以计算机作为教、学、研工具己成必然，选择适当的内容，适时地把数学软件融入到数学课程中进行教学绘图，就有着重要的现实意义了，它不仅为教师和学生提供了一个“活”的教与学的平台，而且也使师生能够在该平台里动态地探索和研究数学问题。[1]
极限是高等数学最重要的内容之一，它是高等数学后续章节的基础。极限学习的好坏，将直接影响着高等数学的学习。在传统的教学模式下，对于大部分学生来说极限是很难理解的一个概念论文开题报告范例。但在教学中引入数学软件Mathematica后，问题就迎刃而解了。
软件Mathematica是一套专门进行数学计算的软件，其强大的数值计算、符号计算、函数绘图等功能对高等数学的教学和学习将起到重要作用。
1 极限概念的理解
例1 观察数列 的前1000项变化趋势。[2]
首先，我们以数值的方式来说明这一变化趋势。输入以下语句[3], 并观察其数值结果，如图1.
图1 数值输出结果（限于篇幅以步长为20输出）
结果表明：随着 的增大，趋近于1绘图，即 .
接下来，我们用图形的方式观察。输入以下语句, 观察其图形变化趋势，如图2.
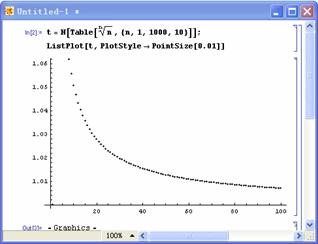
图2 的散点图
从图形可以看出这个数列收敛于1.
例2 通过动画观察当 时数列 的变化趋势。
输入以下命令[4]：
aa={1,1/2^2,1/3^2};
Do[aa=Append[aa,N[1/i^2]];
ListPlot[aa,PlotRange->{0,1},PlotStyle->PointSize[0.02]],{i,4,40}]
运行结果，将输出37个图形，从中节选5个图，如图3.
  
 
图3 的散点图
在Mathematica中双击任意一个图就可以把这37个图用动画的方式放出来，从动画中可以看出所出现的点逐渐接近于 轴，即 .
2 两个重要极限的理解
例3 第一个重要极限
绘出 的图形并输入命令Limit，运行结果，如图4.
图4的图形与极限
观察图形，当 时函数值的变化趋势与用函数Limit求出的结果一致绘图，都为1.
例4 第二个重要极限
绘出 的图形并输入命令Limit，运行结果，如图5.
图5 的图形与极限
在In[7]的第一行是绘制函数的图形，将图形文件存在变量g1中；第二行是绘制常数 （2.71828……）这条直线。观察图形，当 时函数值的变化趋势与用函数Limit求出的结果一致，都为.
3 左右极限
例5 考察函数 在和时的变化趋势论文开题报告范例。
先画出函数的图形，如图6.
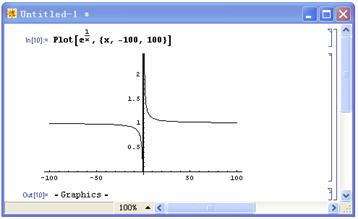
图6函数的图形
由图可以看出，在时， .而时，需要考虑在 时的左右极限了。
我们应用函数Limit求极限，输入命令绘图，运行得出结果，如下：
In[11]=Limit[,x->0,Direction->+1]
Limit[,x->0,Direction->-1]
Out[11]= 0
Out[12]= 
注：命令“Direction->+1”表示自变量x沿x轴的正方向趋向于0,即左极限；
命令“Direction->-1”表示自变量x沿x轴的反方向趋向于0,即右极限。
即时， 的极限不存在。
4 结束语
数学软件Mathematica的在极限教学中的应用，从教学内容、教学形式、教学方法和手段上讲，都是对传统数学教学的一种发展和补充[5]，使学生在掌握知识的同时，也使数学课堂更加开放和更具有活力。
参考文献：
[1]周木生，王庚.数学软件融入到微积分教学中的模式初探[J].重庆师范大学学报（自然科学版）, 2005，22(1):79-80.
[2]吴赣昌.微积分（经管类）[M].北京：中国人民大学出版社，2006.10.
[3]嘉木工作室.Mathematica应用实例教程 [M].北京:机械工业出版社，2002.3.
[4]洪恩维.数学运算大师Mathematica4[M].北京：人民邮电出版社，2002.6.
[5]张颖.数学软件在高职数学实验课中的应用[J]. 高师理科学刊, 2009，29(6):92-94.
|
