基于伊藤过程对股票价格的模拟和预测_布朗运动

二、伊藤过程用于模拟股票价格

连续时间价格过程可以通过取一系列小段时期，然后一期一期地往前推移进行模拟。一共有两种方法可以模拟出价格过程，但他们都不是严格等价的。这两种方法一样好，可以证明看他们的差从长期是趋近于零的。本文仅选取其中一种进行模拟实验。

（一）推导

由倍数形式，可以得到离散形式的方程：

进而可以推出：，这也是倍数模型，但随机系数是对数正态的。

（二）实验

假设一种股票，其初始价格，股票价格由如下几何布朗运动过程决定：

选取基本的时间间隔为一个月，即。下面通过用上文中介绍的模型模拟出三年的股票价格，一共进行100次模拟。

首先布朗运动，将股票价格的几何布朗运动过程对应伊藤过程方程，容易看出，。由，可以求出。至此，便能够得到价格动态过程的模拟方程为：

这样，每生成一组正态随机数，我们就可以对股票价格进行一组模拟运算论文格式范文。

本文最终得到了100组三年股票价格的模拟数据，以下所示为其中一次模拟结果的图表：

表1股票价格动态的模拟

三、伊藤过程用于预测

以“工商银行”（601398）作为估计对象（选取该股票是因为其属大盘股，非市场因素的影响相对较小），取该股票自2009年7月1日至2010年2月12日的开盘价作为样本数据，共有154个样本点，单位时间段为一天，即。第一天时，股价的对数为。

对样本数据取对数后，计算样本数据的平均值和标准差分别为

取和分别作为正态分布总体均值和方差的无偏估计，则可以得出在的时间段内预期收益率和波动率的估计值，即：

解出，，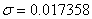

则有：

利用上述估计出的参数，由股票价格变动的马可夫性可知：

可以用其对股票的变化区间做出预测。当置信水平为95%时，则由区间估计不难得出，以95%的置信水平落在区间

内。

首先取时间段内的五个点来进行验证。对于t=20，50，80，110，140五个点，相关数据如表2所示。

表2样本数据

依据伊藤过程，在95%置信水平下，这五天中股价变动的置信区间如表3所示。

表3置信区间

对于未来某段时间内股价的变化，可采用此过程进行预测。取点t=155，156，157，158，159。在95%置信水平下，对此五个点的预测区间如表4所示。

表4预测区间

此五个点上股价的实际值及其对数如见表5所示。

表5实际股价及其对数

伊藤过程预测效果如下图所示。

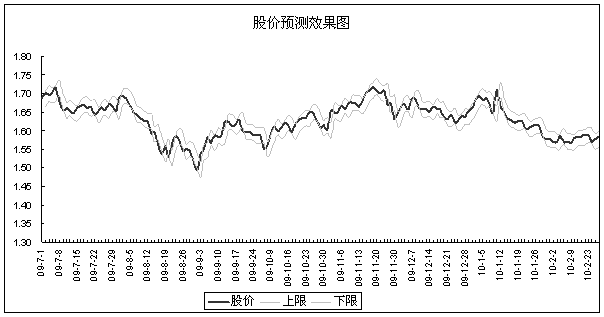
很明显，在时，数据的检验效果很好，而在时，预测效果则相对差一些。这是由于用于预测时，伊藤过程仍采用了前一时间段内的预期收益率和波动率参数来近似预测时间段内的参数。如果能够获取准确的总体预期收益率和波动率参数，伊藤过程将能够收到较好的预测效果。

参考文献
[1]David G.Luenberger. InvestmentScience[M]. 牛津大学出版社，1998.
[2]于庆年.股票价格对数正态分布的实证研究[J]. 辽宁财专学报，1999（4）.
 

 2/2   首页 上一页 1 2