| (一)面板单位根检验
本文对面板数据的单位根检验采用两种方法。一种是相同根情形下的单位根检验,这类检验方法假设面板数据中各截面序列具有相同的单位根过程,采用LLC检验(Levin、LinandChu,2002)、Breitung检验(Breitung,2000);另一类允许面板数据中各截面序列具有不同的单位根过程,主要的检验方法采用IPS检验(Im、PesaranandShin,2003)、Fisher-ADF(MaddalaandWu,1999;Cho,i2001)。单位根检验的滞后期选择我们采用Schwarz标准自动选择。本文所用变量的面板单位根检验结果如下:
Lnwater,lngas,lnsolid的LLC,IPS,ADF-Fisher,PP-Fisher检验都是不显著的,不能拒绝存在单位根原假设,因此Lnwater,lngas,lnsolid序列是非平稳的。Lnwater,lngas,lnsolid的差分△lnwater,△lngas,△lnsoid的LLC,IPS,ADF-Fisher,PP-Fisher检验都是显著的,拒绝原假设。因此,△lnwater,△lngas,△lnsoid是平稳的,即Lnwater,lngas,lnsolid是一阶单整的。
Lnpgdp的Breitung、IPS、ADF-Fisher检验都不显著,但是△lnpgdp的LLC、Breitung、PP-Fisher都是显著的,考虑到各种检验的差异性,可以认为△lnpgdp是平稳的,即Lnpgdp是一阶单整的。
 的Breitung、IPS、ADF-Fisher、PP-Fisher检验是非显著的,因此是非平稳的。 的Breitung、IPS、ADF-Fisher、PP-Fisher检验是非显著的,因此是非平稳的。
△ 的五个检验中只有IPS检验是非显著的,所以△ 的五个检验中只有IPS检验是非显著的,所以△ 是平稳的, 是平稳的, 是一阶单整的。 是一阶单整的。
 的Breitung、IPS、ADF-Fisher、PP-Fisher检验是非显著的,而△ 的Breitung、IPS、ADF-Fisher、PP-Fisher检验是非显著的,而△ 的LLC、ADF-Fisher、PP-Fisher都是显著的,可以认为 的LLC、ADF-Fisher、PP-Fisher都是显著的,可以认为 是一阶单整的。 是一阶单整的。
由面板单位根检验可知,lnwater,lngas,Lnsolid,lnpgdp, , , 都是一阶单整的,可以进行面板协整分析。 都是一阶单整的,可以进行面板协整分析。
表2面板数据单位根检验结果
|
|
LLC
|
Breitung
|
IPS
|
ADF-Fisher
|
PP-Fisher
|
|
lnwater
|
-1.26894
|
_____
|
0.6790
|
0.2389
|
0.0030
|
|
△lnwater
|
-12.0973***
|
_____
|
-6.01628***
|
67.0971***
|
109.720***
|
|
lngas
|
0.08272
|
_____
|
2.47750
|
5.33326
|
8.35091
|
|
△lngas
|
-8.52475***
|
_____
|
-4.68676***
|
56.1003***
|
70.6563***
|
|
lnsolid
|
1.19332
|
_____
|
3.42715
|
8.43921
|
4.19882
|
|
△lnsoid
|
-5.59947***
|
_____
|
-2.52079***
|
35.4996***
|
54.1465***
|
|
lnpgdp
|
-4.81408***
|
4.67410
|
-0.08176
|
20.9193
|
29.3663**
|
|
△lnpgdp
|
-5.08068***
|
-1.48765*
|
-0.41808
|
21.7917
|
37.2352***
|
|

|
-3.91005***
|
5.31492
|
0.59234
|
14.7834
|
26.2334
|
|
△
|
-7.43718***
|
-1.38754*
|
-0.91006
|
28.1347**
|
35.6477***
|
|

|
-1.72209**
|
4.85246
|
1.97321
|
4.67608
|
21.6918
|
|
△
|
-7.73982***
|
-1.17665
|
-1.05131
|
30.1149**
|
36.6116***
|
注:△表示该变量的一阶差分;***、**、*分别表示在1%、5%、10%的水平上显著。
(二)面板协整检验
面板协整检验采用Engle和Granger(1987)的方法。本文应用Pedroni(1999)构造了7个检验面板变量协整关系的统计量来进行检验。其中PanelvPanelρ、PanelPP和PanelADF4个统计量是用联合组内维度(within-dimension)描述,另外3个Groupρ、GroupPP和GroupADF统计量用组间维度(betweendimension)描述。Pedroni认为,七个标准化的统计量都趋于正态分布,但在小样本情况下,PanelADF和GroupADF统计量的检验效果更好,因此在检验结果不一致时,要以这两个统计量为标准。分别以lnwater,lngas,lnsolid为污染物的协整检验结果如表3所示:
在lnwater,lngas,lnsolid为污染物协整检验中,除了组间维度的Panelρ检验不显著外,其他的统计量都是在10%的概率下是显著的。而且PanelADF和GroupADF统计量的检验是在1%的概率下拒绝了不存在协整关系的原假设,可以认为民族地区的污染物lnwater,lngas,lnsolid分别和lnpgdp, , , 之间存在显著的协整关系。 之间存在显著的协整关系。
表3变量的面板协整检验结果
|
|
lnwater
|
lngas
|
lnsolid
|
|
Statistic
|
Prob
|
Statistic
|
Prob
|
Statistic
|
Prob
|
|
组内维度
|
Panelv
|
-2.246557
|
0.0320
|
-2.308407
|
0.0278
|
-2.304350
|
0.0280
|
|
Panelρ
|
0.976436
|
0.2477
|
1.062147
|
0.2270
|
1.312610
|
0.1686
|
|
Panel PP
|
-12.24165
|
0.0000
|
-14.29019
|
0.0000
|
-8.065865
|
0.0000
|
|
Panel ADF
|
-5.394848
|
0.0000
|
-4.685218
|
0.0000
|
-6.485236
|
0.0000
|
|
组间维度
|
Groupρ
|
1.983974
|
0.0557
|
2.246642
|
0.0320
|
2.537138
|
0.0160
|
|
GroupPP
|
-15.90002
|
0.0000
|
-18.32595
|
0.0000
|
-15.40236
|
0.0000
|
|
GroupADF
|
-7.885377
|
0.0000
|
-7.058086
|
0.0000
|
-7.069242
|
0.0000
|
四、模型设定形式检验
面板数据的估计模型有混合模型、变截距模型以及变系数模型三种。因此,对面板数据进行估计时,需要对所建立的模型进行检验,检验样本数据符合变系数模型(2),变截距模型(3)与混合模型(4)中的哪一个,防止模型设定误差导致的估计结果的偏差。即检验如下两个原假设:
H :模型(2)中的解释变量系数对于所有截面成员(八省区)都是相同的(斜率系数是齐性的),但截距项是不同的,即该模型是变截距模型(3); :模型(2)中的解释变量系数对于所有截面成员(八省区)都是相同的(斜率系数是齐性的),但截距项是不同的,即该模型是变截距模型(3);
H :模型(2)中的解释变量系数和截面系数项都是相同的,即该模型为混合模型(4)。 :模型(2)中的解释变量系数和截面系数项都是相同的,即该模型为混合模型(4)。
lny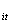 =α =α +β +β lnpgdp lnpgdp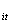 +β +β (lnpgdp (lnpgdp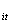 ) ) +β +β (lnpgdp (lnpgdp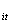 ) ) +u +u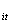 (2) (2)
lny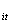 =α =α +β +β lnpgdp lnpgdp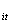 +β +β (lnpgdpc (lnpgdpc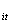 ) ) +β +β (lnpgdp (lnpgdp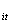 ) ) +u +u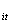 (3) (3)
lny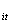 =α+β =α+β lnpgdp lnpgdp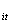 +β +β (lnpgdp (lnpgdp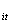 ) ) +β +β (lnpgdp (lnpgdp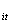 ) ) +u +u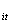 (4) (4)
i=1,2,…,8;t=1999,2000,2001,2002,…,2008.
模型形式检验根据以下两个F统计量:
F = = ~F[(N-1)(K+1),NT-N(k+1)];(5) ~F[(N-1)(K+1),NT-N(k+1)];(5)
F = = ~F[(N-1)k,NT-N(k+1)];(6) ~F[(N-1)k,NT-N(k+1)];(6)
其中N为截面成员的个数,本文为8;T是观察期数,本文为10;k是非常数项解释变量的个数,本文为3;,S ,S ,S ,S ,S 分别是模型(2),(3),(4)的回归残差和。 分别是模型(2),(3),(4)的回归残差和。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


