| ,那么
 对于随机利润 对于随机利润 和已给零售商风险 和已给零售商风险 ,随机利润 ,随机利润 的条件在险价值可以写成 的条件在险价值可以写成
 对于零售商面临的依赖价格的随机需求,这里我们考虑乘法需求模式 对于零售商面临的依赖价格的随机需求,这里我们考虑乘法需求模式

其中, , , ,假定 ,假定 定义在区间 定义在区间 且 且 。 。
2乘法需求模式下具有相同协商权力时的Nash博弈问题
当制造商与零售商具有相同的协商权力时,根据Nash讨价还价模型,制造商和零售商的合作博弈问题可以写成如下形式:
 由于制造商与零售商的最低收益是确定的,因此可以将其最低收益设定为零,该假设不影响解决Nash博弈问题的结果(NagarajanandBassok,2008)。在最低收益记为零时,需要求解如下问题: 由于制造商与零售商的最低收益是确定的,因此可以将其最低收益设定为零,该假设不影响解决Nash博弈问题的结果(NagarajanandBassok,2008)。在最低收益记为零时,需要求解如下问题:

(1)
定理1当供应链成员具有相同的协商权力时,在乘法需求模式中存在均衡解( , , , , )。最优的零售价格 )。最优的零售价格 一定位于区间 一定位于区间 内。并且, 内。并且,
 , ,
 。 。
证明过程见附录。
最优均衡零售价格 由方程 由方程
 决定且唯一(见Chen,XuandZhang2009)。在均衡点 决定且唯一(见Chen,XuandZhang2009)。在均衡点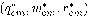 处,可以证明目标函数的海塞矩阵是负定的,从而可知所求的均衡点是稳定的均衡点。 处,可以证明目标函数的海塞矩阵是负定的,从而可知所求的均衡点是稳定的均衡点。
为了衡量供应链利润的相对比例,定义制造商占供应链整体渠道利润的比例如下。
定义1制造商占供应链整体渠道利润的比例为:
性质1假定市场需求噪声 服从 服从 之间的均匀分布,在相同协商权力的Nash合作博弈问题中制造商占整个供应链的利润比例满足 之间的均匀分布,在相同协商权力的Nash合作博弈问题中制造商占整个供应链的利润比例满足 。 。
证明过程见附录。
性质1表明当供应链成员具有相同的协商能力时,在乘法需求模式中制造商占整个供应链的利润比例和在一般随机需求情况下的相同,都与零售商的风险水平 成正比。 成正比。
性质2当市场需求噪声 服从 服从 之间的均匀分布时,均衡批发价格 之间的均匀分布时,均衡批发价格 和均衡零售价格 和均衡零售价格 与 与 无关,而均衡订货量 无关,而均衡订货量 是 是 的增函数。 的增函数。
证明:由于市场需求噪声 服从 服从 之间的均匀分布,则决定最优均衡零售价格 之间的均匀分布,则决定最优均衡零售价格 的方程可化简为 的方程可化简为
。均衡订货量 和均衡批发价格 和均衡批发价格 。显然,均衡批发价格和均衡零售价格与 。显然,均衡批发价格和均衡零售价格与 无关,而均衡订货量是 无关,而均衡订货量是 的增函数。□ 的增函数。□
3乘法需求模式下具有不同协商权力时的Nash博弈问题
上一节主要介绍了在乘法需求模式中具有相同协商权力时Nash博弈问题。然而在分布式供应链中,供应链成员具有不等的协商权力是非常普遍的。这一节主要讨论在分布式供应链中两个供应链成员具有不同协商权力,合作博弈问题建模如下:
 这里 这里 表示零售商的协商权力,其它参数与符号与等协商权力的情况相同。与等协商权力的情况相同,可以将不一致点假定为零而不影响均衡的性质。因此,转换为解决如下问题: 表示零售商的协商权力,其它参数与符号与等协商权力的情况相同。与等协商权力的情况相同,可以将不一致点假定为零而不影响均衡的性质。因此,转换为解决如下问题: (2) (2)
定理2当供应链成员具有不同的协商权力时,如果零售商拥有的协商权力为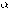 ,那么在乘法需求模式中存在均衡解 ,那么在乘法需求模式中存在均衡解 。最优的零售价格 。最优的零售价格 一定在区间 一定在区间 范围内且 范围内且 。并且, 。并且, , ,
 。 。
证明过程与定理1的证明类似,故省略。
性质3假定市场需求噪声 服从 服从 之间的均匀分布,制造商在零售商具有 之间的均匀分布,制造商在零售商具有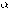 协商权力的Nash合作博弈中占供应链的利润比例为 协商权力的Nash合作博弈中占供应链的利润比例为 。 。
证明过程与性质1的证明类似,故省略。
性质4当市场需求噪声 服从 服从 之间的均匀分布时,均衡零售价格 之间的均匀分布时,均衡零售价格 既与 既与 无关也与 无关也与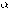 无关,而均衡批发价格 无关,而均衡批发价格 是 是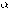 的减函数。 的减函数。
证明:由于市场需求噪声 服从 服从 之间的均匀分布,那么 之间的均匀分布,那么
 0显然,均衡零售价格 0显然,均衡零售价格 既与 既与 无关也与 无关也与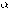 无关。由于 无关。由于
,故均衡批发价格 是 是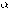 的减函数。□ 的减函数。□
因此,均衡批发价格 与零售商的协商权力 与零售商的协商权力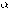 成反比。而零售商均衡的零售价格和均衡的订货量与零售商的协商权力 成反比。而零售商均衡的零售价格和均衡的订货量与零售商的协商权力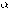 无关。所以,零售商的协商权力 无关。所以,零售商的协商权力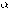 导致均衡批发价格的变化是决定供应链利润分配的关键因素。 导致均衡批发价格的变化是决定供应链利润分配的关键因素。
4数值实验
本文主要研究在乘法需求模式下的Nash合作博弈问题,并证明了当供应链成员具有相同协商权力和具有不同协商权力时都存在均衡解。然而,对于具体的均衡解,我们都假定一个具体的需求噪声分布,为了简化推导本文中采用均匀分布。在这一节中,主要通过数值结果研究制造商在供应链所占得利润比例 和均衡批发价格随零售商风险水平 和均衡批发价格随零售商风险水平 和零售商协商权力 和零售商协商权力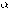 的变化规律。同时,为了研究需求噪声对均衡订货量、均衡零售价格、均衡批发价格及制造商在供应链中所占的利润比例 的变化规律。同时,为了研究需求噪声对均衡订货量、均衡零售价格、均衡批发价格及制造商在供应链中所占的利润比例 的影响,我们比较了需求噪声的两种分布,即均匀分布和正态分布。 的影响,我们比较了需求噪声的两种分布,即均匀分布和正态分布。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


