论文摘要：本文考虑了一个风险厌恶型的零售商面临依赖价格的随机需求的供应链合作博弈问题。零售商以条件在险价值（CVaR）作为其风险衡量，制造商为风险中性，本文首先研究最优均衡批发价格、零售价格和订货量，从而发现在乘法需求模式下具有相同协商权利时的Nash博弈问题和具有不同协商权利时的Nash博弈问题都存在均衡解，并且将乘法需求模式与一般随机需求的情况进行比较分析，发现当需求噪声服从均匀分布时在乘法需求模式下制造商占整个供应链的利润比例和在一般随机需求情况下的一样。
论文关键词：供应链管理,合作博弈,讨价还价,乘法需求模式,条件在险价值
随着顾客对商品需求数量不确定性增加，供应链决策者面临着越来越高的市场不确定性和风险，市场需求不确定情形下供应链决策问题的研究引起了许多研究者的关注。供应链合作博弈的研究通常建立在供应链成员为风险中性的假定基础之上，很少有文献考虑风险厌恶供应链成员的合作博弈问题，而风险厌恶更能反映现实供应链成员的决策行为。此外，零售商经常会面临一种情况，产品的市场需求随其售价变化而变化，故在销售季节之前决策者应决定其零售价格及其订货量。张芳慧，胡支军(2009)研究了由单个风险中性的供应商与单个损失厌恶的零售商组成的两级供应链中，当随机需求依赖于价格时的供应链决策问题，并以乘法需求模式来表示依赖于价格的随机需求，但文章没有考虑CVaR风险度量准则以及供应链协商过程中利润分配问题，因此在供应链环境中，成员如何通过合作博弈分配利润是一个非常具有挑战性的问题。本文主要考虑了一个制造商与一个面临着依赖于价格的随机市场需求的风险厌恶零售商进行协商的单周期问题，且以乘法需求模式来确定零售商的依赖于价格的随机需求，并采用条件在险价值(Conditionalvalueatrisk,CVaR)来度量零售商的风险态度。
本文研究与现有文献的关系体现在以下三个方面：（1)具有风险厌恶成员的供应链决策；（2)供应链的合作博弈；（3）随机需求依赖价格的供应链决策。利润分配的协商过程往往通过Nash博弈模型来解决(Nash,1950)。在供应链管理领域里，建立协商模型通常假定成员是风险中性的。很少有文章在建立协商模型时考虑成员的风险态度。即使有关于成员的风险态度及用条件风险在值(CVaR)作为风险度量标准的研究，也几乎都没有同时考虑到依赖价格的随机需求的情况。马利军等(2010)主要研究在一般随机需求情况（即需求服从某一随机分布而不受其它决策变量的影响）下具有风险厌恶零售商的合作博弈问题，本文是该篇文章的延伸。Chen,XuandZhang(2009)
在CVaR框架下研究带有定价问题的报童模型，给出了加法需求函数及乘法需求函数下最优价格及订货决策存在的条件。而这类文章都没有考虑到供应链协商问题。林志炳等人(2008)在市场需求受价格影响的假设下，建立了一个供应商和零售商都是风险厌恶的两阶段供应链模型，利用确定性等价方法得到分散决策下的最优定价策略。徐晓燕,李四杰(2005)主要研究单周期产品需求不确定情况下的两级供应链的合作问题，并利用市场需求不确定的变异系数来描述其不确定性。但这些文章都没有同时考虑CVaR风险度量准则和供应链的利润分配问题。
本文主要研究在分散的供应链中当零售商是风险厌恶时的均衡行为和利润分配问题，致力于求解并验证随机需求依赖价格的情况下的合作博弈问题中的均衡解。并通过对乘法需求模式与一般随机需求情况进行比较，研究分析制造商占供应链的利润比例与零售商的风险态度、零售商的协商权力的关系。
1模型描述
考虑由一个制造商与一个零售商组成的单周期产品两层供应链。零售商的单位产品零售价格 ，制造商的单位产品生产成本为 ，在销售期末，未满足的需求自动消失，剩余库存的单位残值为 。在协商开始之前所有的信息都是公开的，制造商与零售商协商批发价格为 以及订货量为 。随机价格依赖需求函数 是连续可微且随零售价格严格递减。参考Chen,XuandZhang(2009)对平均需求函数的假定，本文同样假定平均需求函数 是连续、严格递减、二阶可微的非负函数且有递减价格弹性，其定义域是 0， 是最大可容许的零售价格，也就是说，对于所有 都有 。零售商面临的随机需求噪声 的概率分布函数为 ，概率密度函数为 ，并假定随机需求噪声的取值范围为 ，其中 。零售商的风险水平为 ， 。当目标函数中需求是确定型时，最优无风险零售价格 是由方程 决定。为了模型的可解而不失一般性，本文中平均需求函数采用线性函数形式， ，其中 (见GranotandYin2005)。
如果制造商与零售商都参与到协商过程中，那么他们各自从协商中得到的好处一定不少于各自收益的最低要求。各自最低的收益要求也称作不一致点（Nash,1950）。记 零售商收益的最低要求，而 为制造商收益的最低要求。为了避免无意义的情况，假定 。记 分别为一般随机需求情况下等协商权力的博弈问题及不等协商权力的博弈问题中的均衡最优订货量和批发价格，记 分别为乘法需求模式下协商权力相同的博弈问题中的均衡最优订货量、批发价格和零售价格，同样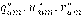 分别为乘法需求模式下不等协商权力博弈问题中的均衡最优订货量、批发价格和零售价格。记 为零售商的利润，记 为制造商的利润。 1/4 1 2 3 4 下一页 尾页 |
