| 形式上,空间滞后模型可以表示为:
 (1) (1)
(1)式中: 是空间自回归系数, 是空间自回归系数, 是误差项(干扰项)向量。 是误差项(干扰项)向量。 可以估计模型中变量的空间相关程度,同时调整其它解释变量的影响。 可以估计模型中变量的空间相关程度,同时调整其它解释变量的影响。
(三)空间误差模型
空间误差模型则反映了区域外溢是随机冲击作用的结果,其考虑了残差项对其它地区经济增长的空间作用,其形式可以表示为:
 , , (2) (2)
这个模型结合了标准回归模型和误差项 的空间自回归模型,同时假设误差项 的空间自回归模型,同时假设误差项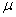 满足条件 满足条件 , ,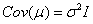 ,即方差固定且误差项是不相关的。 ,即方差固定且误差项是不相关的。
三、模型的建立
(一)模型构建及指标说明
本文使用振兴东北老工业基地实施以来的2005~2008年辽宁省的年度数据,我们用地区历年GDP作为衡量各地级市经济增长水平的指标,在财政支出方面,本文借鉴曾娟红(2005)等的分类方法,主要考察基本建设支出、科教文卫支出、行政支出以及社会保障支出四个方面。基于Devarajan、Swaroop&Zou(1996)的理论分析框架,本文采用柯布-道格拉斯生产函数,并将地方财政的四项支出全部纳入模型中进行分析,其生产函数为: 。在生产函数式中,y代表国内生产总值,k代表私人资本, 。在生产函数式中,y代表国内生产总值,k代表私人资本, 代表第j类政府公共资本或公共服务水平。对生产函数式两边分别取自然对数,可得 代表第j类政府公共资本或公共服务水平。对生产函数式两边分别取自然对数,可得 。该方程式便是本文进行实证分析的基本模型,考虑到劳动力因素,本文最后所建立的实证模型如下式: 。该方程式便是本文进行实证分析的基本模型,考虑到劳动力因素,本文最后所建立的实证模型如下式:
 (3) (3)
其中: 代表辽宁省所包括的14个地级市,t代表年份, 代表辽宁省所包括的14个地级市,t代表年份, 代表随机干扰项,以上是传统意义上的函数,由于传统的模型在经典的高斯马尔可夫假设条件下才适用,若模型存在空间相关性,随机扰动项不再是均质的,如果仍然采用传统的计量模型,可能会导致模型设定偏误和估计结果的不准确。根据以上所述的空间滞后模型和空间误差模型,本文在(3)式中加入了空间因素来构造空间计量模型,即所采用的空间滞后模型为: 代表随机干扰项,以上是传统意义上的函数,由于传统的模型在经典的高斯马尔可夫假设条件下才适用,若模型存在空间相关性,随机扰动项不再是均质的,如果仍然采用传统的计量模型,可能会导致模型设定偏误和估计结果的不准确。根据以上所述的空间滞后模型和空间误差模型,本文在(3)式中加入了空间因素来构造空间计量模型,即所采用的空间滞后模型为:
  (4) (4)
空间误差模型为:
  (5) (5)
其中: 为空间权重矩阵,空间权重矩阵的选择对任何空间统计分析的结果而言,都是一个重要的决定因素。对于空间权重矩阵 为空间权重矩阵,空间权重矩阵的选择对任何空间统计分析的结果而言,都是一个重要的决定因素。对于空间权重矩阵 的计算和设定,常用的主要有两种方法:一种是一阶地理相邻权重矩阵,即相邻空间单位的权重为1,其它为0;另一种是距离权重矩阵,即设定某一距离为门限值,大于该距离就设定为0,小于该距离就设定为1。由于辽宁省各地级市面积相对较小,且各城市相对密集,因此在本文中,不采用地理距离权重矩阵,而采用一阶地理相邻权重矩阵,即:相邻地区取1,不相邻则取0。 的计算和设定,常用的主要有两种方法:一种是一阶地理相邻权重矩阵,即相邻空间单位的权重为1,其它为0;另一种是距离权重矩阵,即设定某一距离为门限值,大于该距离就设定为0,小于该距离就设定为1。由于辽宁省各地级市面积相对较小,且各城市相对密集,因此在本文中,不采用地理距离权重矩阵,而采用一阶地理相邻权重矩阵,即:相邻地区取1,不相邻则取0。
在上式中,因变量 表示地区i第t年的真实经济增长,为了提高实证分析的灵敏度,又因为财政支出对经济增长的影响有一定的滞后期,我们将以真实GDP的四年移动平均值为因变量进行截面数据的空间计量回归分析,自变量 表示地区i第t年的真实经济增长,为了提高实证分析的灵敏度,又因为财政支出对经济增长的影响有一定的滞后期,我们将以真实GDP的四年移动平均值为因变量进行截面数据的空间计量回归分析,自变量 表示i地区第t年的第j类财政支出,从 表示i地区第t年的第j类财政支出,从 ~ ~ 按顺序分别为:政府基本建设支出、科教文卫支出、行政支出以及社会保障支出。 按顺序分别为:政府基本建设支出、科教文卫支出、行政支出以及社会保障支出。 表示i地区第t年的真实社会固定资产投资; 表示i地区第t年的真实社会固定资产投资; 表示i地区第t年的就业人数; 表示i地区第t年的就业人数; 表示i地区第t年的残差;c为常数项。文中所有变量均用我国历年消费价格指数进行平减。另外,为了消除异方差、提高估计精度,对所有数据均取自然对数,有关经济变量数据均来自历年《辽宁统计年鉴》(1995~2008年)。 表示i地区第t年的残差;c为常数项。文中所有变量均用我国历年消费价格指数进行平减。另外,为了消除异方差、提高估计精度,对所有数据均取自然对数,有关经济变量数据均来自历年《辽宁统计年鉴》(1995~2008年)。
(二)模型估计方法和选取原则
由于空间相关具有双向或者多方向的性质,如果用传统的OLS方法去估计带有滞后因变量或序列相关的模型,参数的OLS估计结果将是有偏的。因此,需要考虑其它估计方法,Ord(1975)首先提出了空间滞后和空间误差模型的极大似然估计(ML估计)法,本文在进行模型估计时也采用此估计方法。在模型结果估计出来后,我们不能辨别出是空间滞后模型较优,还是空间误差模型较优,这就涉及到模型选择的问题,常用的模型选择标准有两种:一、根据Anselin(2004)提出的判别准则,可通过对统计量 、LMLAG统计量和LMError统计量的检验来判别,哪种模型的统计量绝对值越大,显著水平越高,就采用哪种模型。二、在LMLAG统计量和LMError统计量都无法辨别模型优劣的条件下,一般对两个模型的极大似然估计量(LogL)、赤迟信息量(AIC)和施瓦茨信息量(SC)进行比较,LogL越大、AIC和SC值越小,说明模型越优。 、LMLAG统计量和LMError统计量的检验来判别,哪种模型的统计量绝对值越大,显著水平越高,就采用哪种模型。二、在LMLAG统计量和LMError统计量都无法辨别模型优劣的条件下,一般对两个模型的极大似然估计量(LogL)、赤迟信息量(AIC)和施瓦茨信息量(SC)进行比较,LogL越大、AIC和SC值越小,说明模型越优。
四、空间计量模型的应用分析
(一)空间相关性检验
为了更深入的揭示辽宁省各地区经济发展集聚与空间差异格局及其影响因素,我们采用空间计量的Moran指数法测算和检验各地级市经济增长在空间上的相关性。在进行空间计量分析以前,首先要对地区间的空间相关性进行检验,空间相关性检验主要应用的是 指数,这里我们采用一阶ROOK空间权重矩阵的全域Moran指数对辽宁省十四个地级市数据做全局空间自相关检验,以分析其是否存在空间相关性(集聚性和异质性),这种方法允许我们通过计算临近城市之间经济增长水平相互关系的空间自相关指数,进而测算并估计各城市间的空间临近效应和空间依赖性。 指数,这里我们采用一阶ROOK空间权重矩阵的全域Moran指数对辽宁省十四个地级市数据做全局空间自相关检验,以分析其是否存在空间相关性(集聚性和异质性),这种方法允许我们通过计算临近城市之间经济增长水平相互关系的空间自相关指数,进而测算并估计各城市间的空间临近效应和空间依赖性。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


