论文导读::科学地预测城市需水量对城市的发展具有十分重要的意义。本文采用BP人工神经网络方法对阿克苏城市需水量进行预测,取得了满意的效果,论证了此种预测方法的可行性和有效性。
论文关键词:BP神经网络,城市需水量,预测
随着城市规模的不断扩大和工农业的迅速发展,城市对水资源的需求在日益提高。在此背景下,对城市需水量进行科学合理地分析和预测就显得尤为重要了。关于城市需水量预测的模型很多,较为典型的有多元回归分析模型、时间序列预测模型、指数法预测模型等。但国外发达国家城市需水发展表明,城市需水并不是一个单调递增的时间序列,而是呈现出先上升到一定峰值、然后下降到一定程度后趋于平稳的变化过程。因此,基于时间序列外推的传统的需水量预测模型存在很大的局限性,受到了一些质疑。本文采用人工神经网络模型进行城市需水量的预测,在精确预测城市需水量的研究领域做了一些尝试。
一 BP神经网络模型
人工神经网络(Artificial Neural Networks, ANN)是一门比较年轻的学科,也是当前国际学术界最为活跃的前沿研究领域之一,其应用领域十分广泛,包括模式识别(语音和图像识别)、经济管理和优化控制、股市分析故障诊断和系统预测等许多领域[1]。
人工神经网络的模型现在有数十种之多,其中BP神经网络(Back-Propagation neural network)模型是最为典型,应用最多的一类模型,约有80%的神经网络属于BP神经网络。它是一种多层前向网络,采用最小均方误差学习方式,需要有教师训练[2]。
BP (BackPropagation)神经网络由输入层、隐层、输出层组成,隐层可以是一层杂志网,也可以扩展为多层。相邻两层之间各神经元进行全连接,而每层各神经元之间无连接。其拓扑结构如图1所示。BP神经网络模型的计算过程可大致分为两个:信息的正向传播过程和误差的反向传播过程。输入样本进入输入层,经过逐层阈值与权值的调整计算,通过隐层传播到输出层,得出各神经元的实际输出。比较实际输出与期望输出,若它们的误差未达到允许值,则进入误差的反向传播过程。按减小希望输出与实际输出误差的方向,从输出层经各中间层逐层修正各连接权,回到输入层。此过程反复交替进行,直至网络的全局误差达到给定的允许值,即完成学习的过程。

图1 BP神经网络模型
二BP神经网络的算法
BP神经网络的计算步骤大致为:
1网络初始化,给各阀值和连接权值分别赋一个区间 内的随机数,设定误差函数 内的随机数,设定误差函数 ,给定计算精度值 ,给定计算精度值 和最大学习次数 和最大学习次数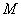 。 。
2 提供训练样本 和期望输出 和期望输出

3计算隐层各神经元的输入和输出


4计算输出层各神经元的输入和实际输出

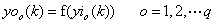
5利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数 , ,

6利用隐层到输出层的连接权值、输出层的 和隐层的输出计算误差函数对隐层各神经元的偏导数 和隐层的输出计算误差函数对隐层各神经元的偏导数 , ,
7利用输出层各神经元的 和隐层各神经元的输出来修正连接权值 和隐层各神经元的输出来修正连接权值 , ,
 ,其中 ,其中 为步长 为步长
8利用隐层各神经元的 和输入层各神经元的输入修正连接权 和输入层各神经元的输入修正连接权 , ,
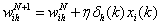 ,其中 ,其中 为步长 为步长
9 计算全局误差
10判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。否则,选取下一个学习样本及对应的期望输出,返回到第三步,进入下一轮学习。
理论上,一个三层BP网络,只要隐层神经元数目足够多,就能以任意精度逼近一个非线性函数,达到预期的效果。但神经元数目的增加也必然会导致计算量的急剧增加,在实际操作过程中,借助Matlab神经网络工具箱可以起到事半功倍的作用。
三 阿克苏市城市需水量预测
阿克苏市位于塔里木盆地西北边缘,地处中纬度欧亚大陆腹地。农业灌溉用水主要依赖于阿克苏老大河和多浪渠,水资源比较丰富,但随着阿克苏河流域限额用水制度的不断完善和工业化、城镇化、农牧产业化进程的不断推进,全市实际可利用水资源量仅为8.36亿m3(其中地表水可利用水资源量6.86亿m3,地下水可利用水资源量1.5m3),实际人均占有可利用水资源量只有1798m3,远低于全国2177m3的人均水平;实际亩均占有可利用水量只有778m3杂志网,远低于全国亩均水量1430m3的水平,水资源供需矛盾十分突出。因此,正确地预测需水量对于本地区社会经济和环境的协调发展具有重要意义。
1 模型建立
依据Kolmogorov定理[3],对于任意连续函数 ,可以有一个三层网络来精确实现它,网络的第一层有m个单元,中间层有2m+1个单元,第三层有n个单元。根据表1所提供的信息,文章建立了一个三层BP神经网络结构。其中输入层为7个神经元,输出层为1个神经元,隐层含15个神经元。 ,可以有一个三层网络来精确实现它,网络的第一层有m个单元,中间层有2m+1个单元,第三层有n个单元。根据表1所提供的信息,文章建立了一个三层BP神经网络结构。其中输入层为7个神经元,输出层为1个神经元,隐层含15个神经元。
表1 阿克苏市1996-2005年用水量及其影响因子[4]
|
年份
|
GDP
/104元
|
人均GDP
/元
|
固定资产
投资/104
|
元工业
个数
|
城市人口
/104人
|
供水总量
/104m3
|
人均日生活
用水量/L●d-1
|
用水量
/104m3
|
|
1996
|
284357
|
5348
|
57389
|
85
|
20.87
|
2218
|
186.3
|
7418
|
|
1997
|
296589
|
5679
|
62798
|
100
|
21.65
|
2435
|
190.5
|
7539
|
|
1998
|
308975
|
5963
|
68567
|
98
|
21.89
|
2478
|
200.8
|
7856
|
|
1999
|
329264
|
6484
|
72183
|
102
|
22.09
|
2512
|
210.2
|
8105
|
|
2000
|
374962
|
7239
|
84297
|
87
|
22.73
|
2217
|
212.8
|
8554
|
|
2001
|
428333
|
8061
|
127884
|
154
|
24.2
|
2349
|
150.9
|
8913
|
|
2002
|
478919
|
8669
|
150219
|
148
|
25.13
|
2469
|
158.6
|
9297
|
|
2003
|
550625
|
9711
|
150726
|
120
|
25.65
|
2673
|
154.2
|
9631
|
|
2004
|
629609
|
11030
|
154365
|
125
|
26.48
|
2789
|
158.7
|
9990
|
|
2005
|
708302
|
12300
|
170239
|
133
|
26.86
|
2986
|
160.2
|
10351
|
2 模型求解
一般情况下获取的数据样本不能直接用于网络训练,需要进行一定的预处理。在此可以利用向量的归一化处理将数据样本都归一化到区间 之间。网络运行后,再还原数据。 之间。网络运行后,再还原数据。
选取1996 ~2003年的数据为训练样本,用2004~2005年的数据对网络进行检验。同时设定运算次数n=10000以及允许的精度E=0.001等。将训练样本以及参数输入到利用Matlab编制的程序中运算,确定满足精度要求的权值和阈值。BP 网络的训练结果如表2 所示。图2更加直观地描述了该BP神经网络模型的预测能力。
表2 原始数据与预测数据表(*为检测样本)
|
年份
|
原始数据
|
预测数据
|
误差(%)
|
|
年份
|
原始数据
|
预测数据
|
误差(%)
|
|
1996
|
7418
|
7458.7
|
0.55
|
|
2001
|
8913
|
8915.3
|
0.04
|
|
1997
|
7539
|
7550.5
|
0.15
|
|
2002
|
9297
|
9303
|
0.08
|
|
1998
|
7856
|
7858.4
|
0.03
|
|
2003
|
9631
|
9655
|
0.26
|
|
1999
|
8105
|
8099.9
|
-0.06
|
|
2004*
|
9990
|
10144
|
1.54
|
|
2000
|
8554
|
8575.7
|
0.25
|
|
2005*
|
10351
|
10294
|
-0.55
|

图2预测结果
通过表2和图2可以看到,该模型具有很好的预测能力。参与训练的1996 ~2003年的数据实际值与预测值的误差最大为0.55%,其中绝大多数不超过0.1%;参与检测的数据误差相对要大一点,但最大误差也只有1.54%(2004年的数据)。
四 结论
BP神经网络模型因其很好的逼近特性、较强的泛化能力和较好的容错性,在越来越多的领域得到了广泛应用。从本文来看,BP神经网络模型作为一种新方法,在城市需水预测领域同样有着巨大的开发潜力与应用前景。
参考文献:
[1]葛哲学,孙志强.神经网络理论与MATLABR2007实现[M].北京:电子工业出版社,2007.
[2]汪晓银,周保平.数学建模与数学实验[M].北京:科学出版社,2010.
[3]洛伦茨G .函数通近论[M].谢庭藩,施威亮译.上海:上海科学技术出版社,1981
[4]邱红霞.基于主成分回归的阿克苏市城市需水量预测[J].地下水,2010,32(2):97-99
|


