量子点内库仑相互作用强度取 ; ; ;双量子点内能级分别取 ;双量子点内能级分别取 其中 其中 由粒子数算符 由粒子数算符 决定,通过式子 决定,通过式子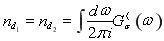 ,自洽求解出 ,自洽求解出  ;选择 ;选择 作为能量单位, 作为能量单位, 作为电导单位。当温度为零时,电流公式化为 作为电导单位。当温度为零时,电流公式化为

M—CQD—M耦合系统的I—V特性曲线如图2.1所示。
扶手椅型CN具有供电子输运的多通道,保证当CQD能级与电极通道相匹配时,电子可隧穿耦合系统,又因为中心CQD存在四个电子的隧穿通道,所以电子共振输运通过CQD有关的主要传导特性都展现在4个主峰上,电子在电极中的量子行为使主共振峰被分裂,组成许多共振边峰。

(图2.2)M—CQD—CN耦合系统在无微波外场时的电流图象
从图2.2我们可以看到单壁碳纳米管电极作为量子线,比起普通电极可以为电子隧穿提供更多通道。在I—V特性曲线中微台阶对应于电子的共振隧穿过程。计算过程中取U=15meV,偏压范围取 。整个耦合系统的输运特性深刻的依赖于电极的DOS,中心耦合量子点的能级结构,源漏偏压等等的影响。电流的单位取为 。整个耦合系统的输运特性深刻的依赖于电极的DOS,中心耦合量子点的能级结构,源漏偏压等等的影响。电流的单位取为 。 。
当两端都选用CN做电极时,G—eV图象如图2.3所示,我们可以看到更多的峰出现,这进一步说明了单壁碳纳米管比普通金属电极提供更多的隧穿通道。

(图2.3)CN—CQD—CN(lambda=0)耦合系统在无微波外场时电导图象
2.2 有微波外场时双量子点耦合系统的相干输运
目前的纳米器件往往在门,源极或漏极上加有一个角频率为 的微波外场(MWF) 的微波外场(MWF) 。这个含时场会引发非线性光子辅助隧穿[5],并且随时间反演对称性也将破坏。其中造成的边带效应 。这个含时场会引发非线性光子辅助隧穿[5],并且随时间反演对称性也将破坏。其中造成的边带效应 , , 使系统为电子的输运开辟出新的通道。共振边峰以 使系统为电子的输运开辟出新的通道。共振边峰以 进行衰减,其中 进行衰减,其中 是第一阶贝塞尔函数,且 是第一阶贝塞尔函数,且 。这样,MWF的不同信息就被体现在系统隧穿电流和微分电导的特性上,从而达到利用外场进行控制的目的。 。这样,MWF的不同信息就被体现在系统隧穿电流和微分电导的特性上,从而达到利用外场进行控制的目的。
我们考虑的外MWF频率范围在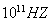 数量级,即光子能量 数量级,即光子能量 (对应的频率为 (对应的频率为 )[4]。针对零温下的微分电导,I—V特性曲线进行数值模拟,以下计算,选择 )[4]。针对零温下的微分电导,I—V特性曲线进行数值模拟,以下计算,选择 作为能量单位, 作为能量单位, 作为电导单位, 作为电导单位, 作为电流单位。 作为电流单位。


(图2.4)M—CQD—M耦合系统在微波外场( )下的电导及电流图象 )下的电导及电流图象
当MWF施加到两极上时,边带效应促使新的通道打开,原来的主峰发生劈裂,构成额外的边峰。劈裂的位置与光子能量 密切相关,由电极能级劈裂引起的光子吸收与发射,即光子辅助隧穿过程。与辅助光子数相联系的电流幅度,随着 密切相关,由电极能级劈裂引起的光子吸收与发射,即光子辅助隧穿过程。与辅助光子数相联系的电流幅度,随着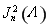 发生迅速衰减。几个光子的吸收和发射就会起很重要的作用(n为参加辅助的光子个数)。 发生迅速衰减。几个光子的吸收和发射就会起很重要的作用(n为参加辅助的光子个数)。

(图2.5)M—CQD—CN耦合系统在微波外场( )下的电导图象 )下的电导图象

(图2.6)CN—QDS—CN耦合系统在微波外场( )下的电导图象 )下的电导图象
光子辅助隧穿的效果强烈依赖于 的大小。由光子能量引起的边带效应使原共振峰被分割,发生整体的劈裂。作为对比我们继续在CN—CQD—CN耦合系统两端施加微波外场( 的大小。由光子能量引起的边带效应使原共振峰被分割,发生整体的劈裂。作为对比我们继续在CN—CQD—CN耦合系统两端施加微波外场( ),可以发现在主峰的两端将有更多的边峰出现。 ),可以发现在主峰的两端将有更多的边峰出现。
3结论
本文运用非平衡格林函数方法对耦合双量子点体系的输运性质进行了研究。总结如下:碳纳米管作为量子线电极具有电子隧穿多通道效应,它拥有的独特态密度结构在系统介观输运中具有支配地位;微波外场的控制对整个系统的量子输运至关重要;其次,当量子点足够小的时候,考虑量子点内库仑相互作用,会出现耦合系统新的隧穿通道。
[参考文献]
[1]Iijima S. Helical microtubles of graphic carbon. Nature(London),354:56-58,1991
[2]Dresselhaus M S, Dresselhaus G.and Eklund P C. Science of Fullerenes and Carbon nanotubes,Academic Press.New York.1996
[3]Geddo M.Ferrini R,Guizzeti G,Patrini M,Franchi S,Frigeri P,Salviati G,and Lazzarini L.Photorefiectance characterization of InAs/GaAs self-assembled quantum dots growm by ALMBE.Eur.Phys.J.B,16:19,2000.
[4]L.-N ZHAO and H.-K ZHAO. Mesoscopic Transport Through A Quantum Dot-Carbon Nanotube System In An Applied Microwave Field.Int. J. Mod .Phys. B.14:2071-2084,2004.
2/2 首页 上一页 1 2 |


