论文导读::可调点-线耦合对双量子点干涉仪中量子输运的影响*,物理论文。
论文关键词:可调耦合,双量子点干涉仪,量子输运
1. 引言
并联耦合双量子点体系是实现量子门,研究交互作用和干涉相互影响的理想人造结构。近年来,因它除了具有与库仑阻塞[1,2]及近藤效应[3-5]相关的丰富的物理现象外,它还可以做为一个Aharonov-Bohm (AB) 干涉仪[6-8]而备受关注。Chi等人研究该结构中磁通有关的隧穿磁阻,结果表明隧穿磁阻的峰值大及方向均由AB环内的磁通调控,且点内库仑力影响调控[9]。对双量子点干涉仪与铁磁电极耦合结构研究,表明负微分电阻依赖于虚过程[10]。最近,日本科学家Hatano指出由两电极引起的间接点间耦合而导致AB振荡周期减半[11]。外加电压[7,12]和电场[13]对双量子点干涉仪结构中量子输运的影响也多有报导。无论是磁通、电极、电压、电场和点间耦合都是研究器件外界影响。但是,就双量子点干涉仪本身结构来看,上下两臂各嵌有一个量子点的AB干涉仪,具有不同空间对称性:(a) 关于垂直轴镜面对称;(b)点对称:旋转 后不变,和(c)关于水平轴镜面对称。这些对称特性必导致电子在并联耦合双量子点中的输运具有奇特的、新颖的量子输运特性。本文通过采用非平衡格林函数方法求解量子输运过程,理论研究了可调点-线耦合对双量子点干涉仪中量子输运的影响。结果表明:调节点-导线间耦合,导致双量子点干涉仪结构对称性和电子传输路径不同,使得电子隧穿并联双量子点结构呈现出一系列的新奇特性,如依赖于点-导线间耦合的线性电导劈裂和点-导线间的耦合强度不同,两量子点中阶梯状的平均电子占据数的分离程度不同,且两台阶的平缓程度也不同。证明了结构决定性能,也为设计可控量子器件提供一个理论依据。 后不变,和(c)关于水平轴镜面对称。这些对称特性必导致电子在并联耦合双量子点中的输运具有奇特的、新颖的量子输运特性。本文通过采用非平衡格林函数方法求解量子输运过程,理论研究了可调点-线耦合对双量子点干涉仪中量子输运的影响。结果表明:调节点-导线间耦合,导致双量子点干涉仪结构对称性和电子传输路径不同,使得电子隧穿并联双量子点结构呈现出一系列的新奇特性,如依赖于点-导线间耦合的线性电导劈裂和点-导线间的耦合强度不同,两量子点中阶梯状的平均电子占据数的分离程度不同,且两台阶的平缓程度也不同。证明了结构决定性能,也为设计可控量子器件提供一个理论依据。
2. 理论模型

图1 双量子点干涉仪模型示意图
采用紧束缚形式的Anderson模型来描述则系统哈密顿量可写为:
 (1) (1)
其中第一行分别为左右两边二维电子气的哈密顿量,εLk和εRp分别表示两边二维电子气的单粒子能级, 为二维电子气中粒子的产生和湮灭算符;第二行为孤立耦合双量子点的哈密顿量,Ui(i=1,2)为量子点内电子间的相互排斥作用; 为二维电子气中粒子的产生和湮灭算符;第二行为孤立耦合双量子点的哈密顿量,Ui(i=1,2)为量子点内电子间的相互排斥作用; 定义自旋态, 定义自旋态, 对应自旋向上, 对应自旋向上, 对应自旋向下; 对应自旋向下; 是量子点中的产生(湮灭)算符, 是量子点中的产生(湮灭)算符, 为点间隧穿耦合,t12表示无磁通量贯穿时两点间的隧穿耦合强度; 为点间隧穿耦合,t12表示无磁通量贯穿时两点间的隧穿耦合强度; 是通过左右两子环的磁通量差对输运电子的相位影响。方程(1)的最后一行为两量子点与左右两边粒子库耦合的哈密顿量。其中 是通过左右两子环的磁通量差对输运电子的相位影响。方程(1)的最后一行为两量子点与左右两边粒子库耦合的哈密顿量。其中  , , , , , ,
 ,tij表示无磁通量贯穿时i和j两部分间的耦合强度; ,tij表示无磁通量贯穿时i和j两部分间的耦合强度; 是通过AB环的总磁通量对输运电子从i运动到j的相位的影响,其中 是通过AB环的总磁通量对输运电子从i运动到j的相位的影响,其中 为磁通量子( 为磁通量子( 示普朗克常数, 示普朗克常数, 是电子电荷); 是电子电荷); 是矢势。为了简单,假定通过AB环的总的磁通量( 是矢势。为了简单,假定通过AB环的总的磁通量( , , 为左右两子环中的磁通量)引起的相移均匀的分布在耦合双量子和AB环的四部分,那么 为左右两子环中的磁通量)引起的相移均匀的分布在耦合双量子和AB环的四部分,那么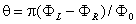 。在第三和第四项的耦合矩阵元中有一个自旋有关的相因子 。在第三和第四项的耦合矩阵元中有一个自旋有关的相因子 是Rashba自旋轨道耦合相互作用的结果,其中 是Rashba自旋轨道耦合相互作用的结果,其中 表示量子点i的尺寸大小, 表示量子点i的尺寸大小, , , 分别为电子的有效质量和相互作用系数。虽然前两项与自旋无关,但为了下面描述的方便也带有自旋下标。 分别为电子的有效质量和相互作用系数。虽然前两项与自旋无关,但为了下面描述的方便也带有自旋下标。
流过两量子点的自旋态为 的电流表达式为: 的电流表达式为:
 (2) (2)
其中 , , 是 Keldysh 格林函数 是 Keldysh 格林函数

(3)

(4)
温度高于近藤温度情况下的量子输运问题,就可以采用Hartree-Fock近似截断得
 (5) (5)
其中
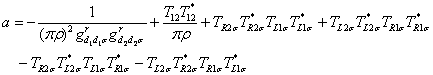 (6) (6)
 (7) (7)
 (8) (8)
同理可以得出:
 (9) (9)
其中
 (10) (10)
 (11) (11)
 (12) (12)
 (13) (13)
当AB环中无磁通量,且不考虑自旋轨道耦合效应时,则点-导线间耦合蜕化为 , , , , , ,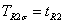 。假定两量子点的能级差为0.5, 。假定两量子点的能级差为0.5, , , ,其它参数取为kBT=0.1, U1=5.0,U2=5.0。 ,其它参数取为kBT=0.1, U1=5.0,U2=5.0。
1/4 1 2 3 4 下一页 尾页 |


