摘要:本论文利用非平衡格林函数理论对微波场辐照下的碳纳米管双量子点耦合系统的相干输运性质进行了较系统的研究。研究发现单壁碳纳米管能够比选用的金属电极提供更丰富的遂穿通道。微波场作用下的光子辅助隧穿(PAT)可以提供新的隧穿通道,实现利用外场控制系统输运的目的。整个系统的输运受电极态密度,系统各部分耦合强度,及量子点内部库仑相互作用的深刻影响,通过人工调节可实现耦合系统的理想遂穿行为。
论文关键词:碳纳米管,量子点,微波场,非平衡格林函数
在介观系统中载流子的运动只经受弹性碰撞,散射前后载流子波函数和相位有确定的关系,相位的相干性没有被破坏,量子力学规律起支配作用。介观区域物理与宏观区域物理有很大区别。随着电子技术的高度发展,超大规模集成电路中单位面积上电子元件数量不断增加,单个电子元件的尺度已能达到介观尺度,量子干涉现象在这样的电子元件中起支配作用。传统的电子器件日益接近其工作极限,全新的量子器件将在未来电子技术中占重要地位。
碳纳米管[1]作为制备纳米电子器件的理想材料,揭开了纳米电子学的新一页,引起了各个不同科研领域广泛兴趣。量子点也是近年来纳米电子学研究的热门课题[2],有望成为模拟和数字电路方面应用的主要纳米电子器件,并在认识相干输运性质与电子间强关联行为方面取得了很大的进展。
本文运用非平衡格林函数理论将电流公式推导出来并进行数值运算,讨论碳纳米管作为电极的物理特性;研究外场作用下系统的电子相干输运;通过自恰计算求解出量子点内部电子占有数,从而发现耦合系统更多的物理现象。
1 系统模型与电流公式
耦合系统电极由金属纳米线和碳纳米管提供,耦合双量子点通过 的自组织生长实现[3],两根导线分别搭接在两个量子点上。采用紧束缚计算处理CN电极。普通金属电极作为自由电子系统研究。决定输运特性的系统总哈密顿量由耦合相互作用项求和构成。双量子点的哈密顿量表示为 的自组织生长实现[3],两根导线分别搭接在两个量子点上。采用紧束缚计算处理CN电极。普通金属电极作为自由电子系统研究。决定输运特性的系统总哈密顿量由耦合相互作用项求和构成。双量子点的哈密顿量表示为
 (1.1) (1.1)
其中  , , 和 和 分别是第 分别是第 个量子点中电子的产生算符和消灭算符, 个量子点中电子的产生算符和消灭算符, 代表第 代表第 个量子点中局域电子的占有数。 个量子点中局域电子的占有数。 是第 是第 个量子点中的能级。 个量子点中的能级。 为第 为第 个量子点中库仑相互作用的强度的大小。双量子点耦合相互作用的哈密顿量为 个量子点中库仑相互作用的强度的大小。双量子点耦合相互作用的哈密顿量为
 (1.2) (1.2)
其中 为耦合双量子点之间电子相互作用强度的大小。左极与左量子点之间耦合哈密顿量为 为耦合双量子点之间电子相互作用强度的大小。左极与左量子点之间耦合哈密顿量为
 (1.3) (1.3)
 为左极与左量子点之间电子相互作用强度的大小。 为左极与左量子点之间电子相互作用强度的大小。 和 和 分别是左极中电子的产生算符和消灭算符。右极与右边量子点之间耦合哈密顿量为 分别是左极中电子的产生算符和消灭算符。右极与右边量子点之间耦合哈密顿量为
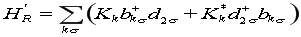 (1.4) (1.4)
 为右极与右量子点之间电子相互作用强度的大小。 为右极与右量子点之间电子相互作用强度的大小。 和 和 分别是右极中电子的产生算符和消灭算符。当两电极分别加上震荡微波场 分别是右极中电子的产生算符和消灭算符。当两电极分别加上震荡微波场  。假设所加在两极上的微波场振幅 。假设所加在两极上的微波场振幅 非常小,没有产生非线性效应,这时两极上的哈密顿量可以写为 非常小,没有产生非线性效应,这时两极上的哈密顿量可以写为
 (1.5) (1.5)
 (1.6) (1.6)
因此微波场中系统总的哈密顿量可以写为
 (1.7) (1.7)
采用Keldysh NGF,定义出左极及右极上推迟(超前)格林函数和kelydesh格林函数。利用第一阶Bessel函数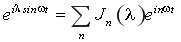 ,可以得到在微波场中两极上的推迟(超前)格林函数,同理得到微波场中两极上的kelydesh格林函数.根据电流连续性方程,可以得到左极电流表达式,然后利用电极与量子点的Dyson方程,并做傅立叶变换可得 ,可以得到在微波场中两极上的推迟(超前)格林函数,同理得到微波场中两极上的kelydesh格林函数.根据电流连续性方程,可以得到左极电流表达式,然后利用电极与量子点的Dyson方程,并做傅立叶变换可得



其中线宽函数




其中

 
 


其中 代表左极反射电流的大小, 代表左极反射电流的大小, 代表左极透射电流的大小, 代表左极透射电流的大小, 代表左极电流反射系数, 代表左极电流反射系数, 代表左极电流的透射系数。同理我们可得到右极电流表达式,右极上的反射电流,右极上的透射电流,右极电流反射系数以及右极电流透射系数。当我们慢慢移去微波场,可得电流的 代表左极电流的透射系数。同理我们可得到右极电流表达式,右极上的反射电流,右极上的透射电流,右极电流反射系数以及右极电流透射系数。当我们慢慢移去微波场,可得电流的 形式,描述电子在耦合双量子点之间的跃迁,电子被两端电势差驱动,当两端电势差为零时,系统处于平衡状态。当没有微波场时,电流只有一个通道,左极及右极透射电流大小分别为 形式,描述电子在耦合双量子点之间的跃迁,电子被两端电势差驱动,当两端电势差为零时,系统处于平衡状态。当没有微波场时,电流只有一个通道,左极及右极透射电流大小分别为


依据Roamo-Shockly 理论 ,得到电流表达式 ,得到电流表达式
 (1.8) (1.8)
其中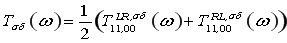
两端电导率 (1.9) (1.9)
当 ,共振峰分别出现在 ,共振峰分别出现在 , ,
 处,峰值大小可以通过计算得到。 处,峰值大小可以通过计算得到。
2 电流特性曲线
本部分数值模拟电流与各物理量随电极与外场变换的响应曲线。考虑无微波外场和有微波外场时系统在弱耦合及宽带近似的输运性质,耦合强度用线宽函数  描述,并设左右两极耦合强度为相等的常数。 描述,并设左右两极耦合强度为相等的常数。
2.1无微波外场时双量子点耦合系统的相干输运
针对零温下的微分电导,I-V特性及电流与偏压间的关系进行数值模拟,当源漏偏压不为零,传输特性可由零温的微分电导描述


 (图2.1)M—CQD—M耦合系统在无微波外场时电导及电流图象 (图2.1)M—CQD—M耦合系统在无微波外场时电导及电流图象
由上一节公式推导可知CQD中包含四个能级 与 与 ,令门电压 ,令门电压 。因中心CQD存在4个供电子隧穿的通道,所以在M—CQD—M耦合系统中可以看到4个峰出现。在这个系统中我们取电极与量子点之间的耦合强度为 。因中心CQD存在4个供电子隧穿的通道,所以在M—CQD—M耦合系统中可以看到4个峰出现。在这个系统中我们取电极与量子点之间的耦合强度为 。量子点之间耦合强度取 。量子点之间耦合强度取 ,对于普通金属,其DOS取为 ,对于普通金属,其DOS取为 。 。
1/2 1 2 下一页 尾页 |


