论文摘要:综合考虑多种电迁移驱动机制, 基于ANSYS软件和FORTRAN程序提出电迁移失效算法, 导出了电迁移灵敏度分析方程, 并建立相应的数值算法. 在此基础上考虑设计变量为激活能、初始自扩散系数和材料力学性能参数等对金属互连焊球进行电迁移灵敏度分析, 同时基于三维有限元分析的全因子试验设计法对CSP封装结构的电迁移寿命进行仿真预测.
论文关键词:电迁移,灵敏度,试验设计,互连焊球,有限元分析
0引言
电迁移(EM)是导电金属材料在通过较高的电流密度时,金属原子沿着电子运动方向进行迁移的扩散现象,它是引起集成电路(IC)失效的一种重要机制.特别是随着微电子技术的迅猛发展,电子器件焊点尺寸及其间距日趋减小,电流密度急剧增加,电迁移现象更易发生,所引起的可靠性问题就更加严重.
电迁移失效问题并非一个孤立的现象,在电迁移过程中往往同时伴随着热迁移、应力迁移和化学迁移等过程.高电流密度产生的焦耳热将形成温度梯度,这种梯度是热迁移的驱动力;电迁移形成的空穴将诱致互连结构内部产生应力,伴随着机械载荷和热载荷引起的应力,这些应力叠加起来将形成应力梯度驱使原子进行迁移.另外,由于迁移导致金属结构内部原子密度不均匀,这种原子密度梯度引起了化学迁移.因此,金属互连结构的电迁移失效问题实际上是在多种迁移机制耦合作用的共同结果.
灵敏度分析是一种评价因设计变量或参数的改变而引起结构响应特性变化率的方法,广泛地用于结构的优化设计.灵敏度分析对于结构的优化设计和可靠性分析至关重要.对于电迁移灵敏度问题,影响因素主要有几何尺寸、材料参数和边界条件等,通过试验设计研究和灵敏度分析,可充分了解不同因素对电迁移特性的影响程度,对于提高焊球抵抗电迁移的能力具有非常重要的意义.因此,本文在前期研究的基础上,进一步研究金属互连焊球电迁移的试验设计仿真和灵敏度分析,为微电子芯片的设计、制造和封装工艺的参数优化提供依据.
1电迁移模拟算法
电迁移是扩散控制的质量输运过程,原子密度的演化方程是典型的质量守恒方程,表达如下:
 (1) (1)
式中,c=C/C为正则化的原子密度,C为真实的原子密度,C为无应力状态(平衡状态)下初始原子密度;t是时间; 是正则化的总原子通量. 是正则化的总原子通量.
总原子通量 可表示为: 可表示为:
 (2) (2)
其中,
 (3) (3)
式中,k为Boltzmann常数;e为电子电荷; 为有效电荷数;T为绝对温度; 为有效电荷数;T为绝对温度; 为电阻率, 为电阻率, ,a金属材料的温度系数, ,a金属材料的温度系数, 为初始温度T所对应的电阻率; 为初始温度T所对应的电阻率; 为电流密度矢量; 为电流密度矢量; 为传输热;W为原子体积; 为传输热;W为原子体积; 为静水压力,s、s、s为三个主应力; 为静水压力,s、s、s为三个主应力;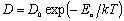 为金属原子的有效扩散速率, 为金属原子的有效扩散速率, 为激活能,D为初始自扩散系数. 为激活能,D为初始自扩散系数.
通常,在边界G上,电迁移演化方程的边界条件和初始条件分别可表示为:
 (4a) (4a)
 (4b) (4b)
基于伽辽金方法,对式(1)进行求解:
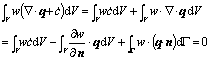 (5) (5)
将式(2)和式(4a)代入,可得:
 (6) (6)
式中,取权函数 ,其中 ,其中 是单元的形函数.假设 是单元的形函数.假设 , , ,经过单元的离散化,可以得到方程(6)的矩阵形式: ,经过单元的离散化,可以得到方程(6)的矩阵形式:
 (7) (7)
引入a族差分格式:
 ,0£a£1(8) ,0£a£1(8)
式中, 是时间步长. 是时间步长.
由式(7)和式(8),可得
 (9) (9)
式中, .(15) .(15)
由给定的电流密度 、温度T、温度梯度?T和静水应力梯度 、温度T、温度梯度?T和静水应力梯度 ,式(1)描述了原子密度的演化过程.为了获得连续的原子密度重分布,假设从一个平衡状态达到一个新的平衡状态过程中,电流、温度和应力是迅速进行重分布的,相对而言原子的迁移是缓慢的.为此,一旦得到了电流、温度和应力分布,我们就可以基于稳态解求解原子密度的演化过程. ,式(1)描述了原子密度的演化过程.为了获得连续的原子密度重分布,假设从一个平衡状态达到一个新的平衡状态过程中,电流、温度和应力是迅速进行重分布的,相对而言原子的迁移是缓慢的.为此,一旦得到了电流、温度和应力分布,我们就可以基于稳态解求解原子密度的演化过程.
具体地,我们通过ANSYS电-热-结构耦合分析获得模型的电流密度分布、温度分布和应力分布,并基于FORTRAN编写的原子密度重分布算法获得不同时刻的原子密度,详尽的算法和分析流程可参见我们以往的论文[6-8].
2电迁移灵敏度分析
电迁移灵敏度分析主要是研究由设计变量引起的原子密度响应的变化率,可简单表示为 ,设计变量 ,设计变量 可取电迁移分析的物理学材料参数、金属材料电、热和机械性能参数以及几何结构尺寸和形状参数等. 可取电迁移分析的物理学材料参数、金属材料电、热和机械性能参数以及几何结构尺寸和形状参数等.
假设用上标“~”表示对设计变量求微分,则 ; ; . .
式(6)对设计变量求微分,可得:
 (10) (10)
方程(10)写成矩阵形式,可以表示为:
 (11) (11)
其中, 为刚度矩阵; 为刚度矩阵; . .
鉴于原子密度灵敏度的时间相关性,采用 族近似加权平均法获取原子密度灵敏度 族近似加权平均法获取原子密度灵敏度 . .
 (12) (12)
式中, 是时间步长.当 是时间步长.当 ,式(12)可简化为 ,式(12)可简化为 ,显然这是前差分格式(显式算法);当 ,显然这是前差分格式(显式算法);当 ,式(12)简化为 ,式(12)简化为 ,这是后差分格式(隐式算法);本文取 ,这是后差分格式(隐式算法);本文取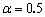 (隐式算法),称为Crank-Nicolson方法,其算法是稳定的且具有O((Dt))精度.对于隐式算法( (隐式算法),称为Crank-Nicolson方法,其算法是稳定的且具有O((Dt))精度.对于隐式算法( ),计算不依赖于时间步长,结果是稳定的;对于显式算法( ),计算不依赖于时间步长,结果是稳定的;对于显式算法( )则不然,只有当 )则不然,只有当 ,式中 ,式中 为 为 的最大特征值,算法才是稳定的. 的最大特征值,算法才是稳定的.
由方程(11)和(12)可得:
 (13) (13)
其中, ; ; 和 和 可由原子密度重分布方程得到,而初始原子密度灵敏度 可由原子密度重分布方程得到,而初始原子密度灵敏度 ,因此由方程(13)可得到每个时间步的原子密度灵敏度 ,因此由方程(13)可得到每个时间步的原子密度灵敏度 . .
进一步,特殊情况下,矩阵 可以简化为: 可以简化为:
 (14) (14)
对于无通量边界条件( ,即在封闭域内原子没有输入和输出),则有 ,即在封闭域内原子没有输入和输出),则有 .当设计变量为材料的力学性能参数时,式(13)可以进一步简化为: .当设计变量为材料的力学性能参数时,式(13)可以进一步简化为:
 (15) (15)
可以发现,基于力学性能参数的灵敏度方程退化为原子密度重分布方程.将初始原子密度灵敏度 代入方程(15),易得 代入方程(15),易得 ,即无通量边界条件下任意时刻原子密度对力学性能参数的灵敏度为0.这表明,金属互连结构的力学性能参数的变化对无通量边界条件下的电迁移没有影响. ,即无通量边界条件下任意时刻原子密度对力学性能参数的灵敏度为0.这表明,金属互连结构的力学性能参数的变化对无通量边界条件下的电迁移没有影响.
为了验证上述电迁移灵敏度分析算法的正确性,以长为l、受恒定电流作用的金属导线为例,并且正则化原子通量仅考虑电子风力和原子密度梯度两种驱动力,则电迁移演化方程中可简化为:
 (16) (16)
其中,x为电场的坐标值.
考虑封闭的边界条件,
 (17) (17)
其中,t为时间.
为计算方便,引入无量纲参数 和 和 ,其中 ,其中 , , , , 具有 具有 的单位, 的单位, 为电迁移的特征长度,即“Blech长度”; 为电迁移的特征长度,即“Blech长度”; 为正则化时间,则电迁移演化方程(16)在阴极处的解析解为: 为正则化时间,则电迁移演化方程(16)在阴极处的解析解为:
 (18) (18)
因此,正则化原子密度关于激活能E和初始自扩散系数D的灵敏度分别为:
 (19) (19)
 (20) (20)
进一步,以截面为7mm′7mm的Al线为例(如图1所示),利用ANSYS有限元软件分析该模型在恒定电流密度为 和温度400K下,基于本文的原子密度重分布算法得到阴极处的正则化原子密度 和温度400K下,基于本文的原子密度重分布算法得到阴极处的正则化原子密度 随时间的变化情况. 随时间的变化情况.
 
图1Al线模型的网格(共350个单元,p=2)
Fig.1MeshofAlwiremodel(350elements,p=2)
图2为无通量边界时不同长度导体在阴极边界上(x=0)的正则化原子密度随时间的变化情况,图中的虚线为根据式(18)取前100项所得的解析解.从图2可以看出,在阴极边界上的解析解和本文的电迁移算法求得的原子密度吻合的很好,充分证明了该算法的正确性.
 
图2不同长度导体在阴极的正则化原子密度变化
Fig.2Normalizedatomicdensityatcathodewiththedifferentlengthsofconductors
以下考虑网格对本文算法的影响.以p=2为例,将Al线模型划分成不同密度的网格,得到不同网格密度情况下阴极边界处的正则化饱和原子密度值,如表1所示.可以看出,本文算法并不依赖网格的划分.另外,表2为单元总数为350时不同时间增量下阴极边界处的正则化饱和原子密度,从表2可以看出,本文算法基本不依赖时间增量,即该算法是稳定的.
表1不同网格密度下阴极的正则化饱和原子密度(p=2)
Table1Normalizedsaturationatomicdensityatcathodewithdifferentmeshdensities(p=2)
|
单元总数
|
无边界通量变化的正则化饱和原子密度
|
误差(%)
|
|
解析解
|
本文算法解
|
|
176
|
2.3230
|
2.3110
|
-0.0865%
|
|
350
|
2.3118
|
-0.0519%
|
|
882
|
2.3123
|
-0.0303%
|
|
2700
|
2.3127
|
-0.0130%
|
表2不同时间增量时阴极处的正则化饱和原子密度(p=2)
Table2Normalizedsaturationatomicdensityatcathodewithdifferenttimeincrement(p=2)
|
p=2
|
无边界通量变化的正则化饱和原子密度
|
|
时间增量: Dt
|
0.001
|
0.01
|
10
|
100
|
|
单元数目: 350
|
2.3118
|
2.3118
|
2.3118
|
2.3118
|
  
图3原子密度关于激活能E的灵敏度比较(p=2)
Fig.3SensitivityofthenormalizedatomicdensitywithrespecttoE(p=2)
  
图4原子密度关于初始自扩散系数D的灵敏度比较(p=2)
Fig.4SensitivityofthenormalizedatomicdensitywithrespecttoDunder(p=2)
图3和图4分别为p=2时阴极处原子密度关于激活能E和初始自扩散系数D的灵敏度比较,其中实线为基于式(19)和式(20)所得的解析解,空心方框为根据本文提出的原子密度重分布算法求得的解.
从图3和图4可以看出,式(19)和式(20)的解析解和本文提出的原子密度重分布算法的数值解吻合良好.这说明本文推导的灵敏度方程和数值算法的正确性和可靠性.不难发现,原子密度关于激活能和初始自扩散系数的灵敏度的最大值所对应的时间是一致的,等于原子密度刚出现饱和值时所对应的时间.
3CSP封装结构的电迁移试验设计研究
试验设计是通过一系列试验及分析方法,有目的地改变系统的输入来观察输出的变化情况,从而呈现设计参数之间的相互关系,确定最优化的设计方案.为了研究CSP封装结构在电流“拥集”下的后端设计规则,本文采用基于三维有限元分析的全因子试验设计法,在电流为1.7A下进行电迁移寿命(TimetoFailure,TTF)的仿真预测.
CSP模型包括芯片、凸点下金属化层(UBM)、铝引线、铜引线以及焊球.其中,UBM共三层,分别为Al、Ni(V)和Cu层.该模型共有36个焊球,间距为500mm,焊球材料为无铅焊料(95SnAg4.5Cu0.5).为了更加准确得研究电迁移的过程,本例将采用ANSYS的子模型技术,在子模型中对易发生电迁移的三个焊球建立详细的焊球结构.相关结构如图5所示,详细的材料参数可参考文献[6].
本文选取4个参数进行试验设计,包括:UBM倾角(如图6所示)、UBM直径、UBM厚度和焊球的形状,详细参数如表3所示.
   
(a)整体结构(b)局部结构
(a)wholestructure(b)localstructure
  
(c)子模型结构(d)焊球详细结构
(c)sub-model(d)detailedsolderbump
图5CSP封装结构图
Fig.5CSPpackagestructure
基于原子密度重分布算法及有限元实施方案,结合表3的全因子试验设计参数,对不同参数组合情况下的电迁移寿命进行了仿真预测.在半导体工业中,通常采用电阻增加了原有值的15%作为金属互连结构的电迁移失效依据,本文也采用此依据作为失效判断的标准.
 
图6UBM倾角示意图
Fig.6SchematicdiagramofUBMrimangle
表3全因子试验的设计参数
Table3DesignparametersofDOE
|
设计参数
|
参数值
|
|
UBM倾角
|
0o、15o、30o、45o、60o、75o、90o
|
|
UBM直径
|
0.09mm、0.11mm、0.125mm
|
|
UBM厚度
|
0.00106mm、0.00212mm、0.00424mm
|
|
焊球的形状
|
球体、圆柱体、立方体、双球体
|
图7和图8分别为不同UBM倾角的电迁移失效时间曲线图和部分UBM倾角的电迁移空洞失效仿真图.从中不难发现,当UBM倾角为75o时,焊球有较高的电迁移失效寿命;在与UBM接触的地方,垂直性凸台结构(如UBM0o倾角和90o倾角)具有较差的抗电迁移能力;0o o时,随着倾斜角度的增大,电迁移寿命也不断增大. o时,随着倾斜角度的增大,电迁移寿命也不断增大.

图7不同UBM倾角的电迁移失效时间曲线图
Fig.7TTFwithdifferentUBMrimangles
 
图8部分UBM倾角的空洞失效仿真图
Fig.8VoidswithsomedifferentUBMrimangles
图9为不同UBM直径的电迁移失效时间曲线图,可以发现,随着UBM直径的增大,电迁移失效寿命也不断增加.
 

图9不同UBM直径的电迁移失效时间曲线图
Fig.9TTFwithdifferentUBMradius
图10为不同UBM厚度的电迁移失效时间曲线图,可以发现,随着UBM厚度的增加,电迁移失效寿命也不断增加.
 

图10不同UBM厚度的电迁移失效时间曲线图
Fig.10TTFwithdifferentUBMthicknesses
为了考察焊球形状对电迁移寿命的影响,本文分别采用了球体、圆柱体、立方体和双球体四种不同形状的焊球.在保证焊球高度一致的情况下,保持焊球体积相同.
表4不同焊球形状的电迁移寿命比较
Table4TTFwithdifferentshapesofsolderball
|
形状
|
TTF(小时)
|
|
双球
|
945.3
|
|
球体
|
1947.2
|
|
圆柱体
|
20458.6
|
|
立方体
|
15941.7
|
 
(a)球体(Spheroid)(b)圆柱体(Cylinder)
 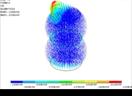
(c)立方体(Cube)(d)双球体(Doubleball)
图11不同形状焊球的电流密度分布图
Fig.11Currentdensitydistributionswithdifferentshapesofsolderball
图11为不同形状焊球的电流密度分布图,表4为不同形状焊球的电迁移寿命比较.由表4并结合图11可知,形状对电迁移寿命有较大的影响,其中圆柱体形状焊球具有最强的抗电迁移能力.虽然近期有学者提出采用双球模型可提高功率循环下的寿命,但从电迁移分析的角度来看,双球模型并非最优结构.
4CSP互连焊球的电迁移灵敏度分析
以下研究CSP互连焊球的正则化原子密度关于激活能E和初始自扩散系数D的灵敏度.图12为4个不同时刻正则化原子密度关于激活能E的灵敏度的分布云图,其最大值(正值)出现在焊球与UBM接触位置(电子流进的位置,即焊球将出现电迁移空洞的位置).这表明,随着激活能E的不断增加,该区域的正则化原子密度呈现不断增加的趋势;图13为4个不同时刻正则化原子密度关于初始自扩散系数D的灵敏度的分布云图.可以发现,焊球与UBM接触位置的灵敏度为负值,这表明,随着初始自扩散系数D的不断增加,该区域的正则化原子密度不断减小.
图14为正则化原子密度对E和D的灵敏度随时间的变化趋势.在焊球与UBM接触位置,正则化原子密度关于激活能E的灵敏度 随时间首先减少而后快速增加,而正则化原子密度关于初始自扩散系数D的灵敏度 随时间首先减少而后快速增加,而正则化原子密度关于初始自扩散系数D的灵敏度 则相反.从灵敏度的数值上可以发现,正则化原子密度对激活能相当敏感,因此在选择无铅焊料时,应尽可能选择激活能较大的材料来抵抗电迁移的发生. 则相反.从灵敏度的数值上可以发现,正则化原子密度对激活能相当敏感,因此在选择无铅焊料时,应尽可能选择激活能较大的材料来抵抗电迁移的发生.
 
(a)1s(b)100s
 
(c)1000s(d)1.57E+6s(失效时间,TTF)
图12正则化原子密度关于激活能E的灵敏度
Fig.12SensitivityofthenormalizedatomicdensitywithrespecttoE
 
(a)1s(b)100s
 
(c)1000s(d)1.57E+6s(失效时间,TTF)
图13正则化原子密度关于初始自扩散系数D的灵敏度
Fig.13SensitivityofthenormalizedatomicdensitywithrespecttoD
 
(a)节点位置和坐标
(a)Nodallocationandcoordinates

(b)正则化原子密度对E的灵敏度随时间的变化
(b)SensitivitiesofnormalizedatomicdensitywithrespecttoEwiththetime

(c)正则化原子密度对D的灵敏度随时间的变化
(c)SensitivitiesofnormalizedatomicdensitywithrespecttoDwiththetime
图14正则化原子密度对E和D的灵敏度随时间的变化
Fig.14SensitivitiesofnormalizedatomicdensitywithrespecttoEandDwiththetime
5结论
本文综合考虑电迁移失效的各种影响因素,针对CSP封装结构的无铅焊球进行了试验设计仿真与灵敏度分析.结果表明,在条件允许下,可以选择UBM直径和厚度较大的圆柱体焊球的封装结构抵抗电迁移的发生;焊球的电迁移对激活能非常敏感,其次是初始自扩散系数,而材料力学性能参数对电迁移影响最小.
参考文献
1 Tu K N. Recent advances on electromigration in every-large-scale-integration of interconnects [J]. Journal of Applied Physics, 2003, 94(9): 5451-5473.
2 Korhonen M A, B?rgesen P, Tu K N, Li C Y. Stress evolution due to electromigration in confined metal lines [J]. Journal ofApplied Physics, 1993, 73(8): 3790-3799.
3 Tan C M, Roy A. Investigation of the effect of temperature and stress gradients on accelerated EM test for Cu narrowinterconnects [J]. Thin Solid Films, 2006, 504 (1-2): 288-293.
4 刘涛, 邓子辰. 考虑材料设计变量的热-固耦合结构的优化设计 [J]. 固体力学学报, 2006, 27(4): 374-378. (Liu T, Deng Z C. The design optimization for thermal2stress coupled structures by considering structural design variables andmaterial design variables simultaneously [J]. Chinese Journal of SolidMechanics, 2006, 27(4): 374-378(in Chinese).)
5 顾元宪, 赵红兵, 陈飚松, 亢战. 热-应力耦合结构灵敏度分析方法 [J]. 力学学报, 2001, 33(5): 685-691. (Gu Y X, Zhao H B, Chen B S, Kang Z. Sensitivity analysis and design optimization of thermal-stress coupled structures [J]. Chinese Journal of Theoreticaland Applied Mechanics, 2001, 33(5): 685-691(in Chinese).)
6 梁利华, 张元祥, 刘勇, 陈雪凡. 金属互连结构的电迁移失效分析新算法 [J]. 固体力学学报, 2010, 31(2): 164-172. (Liang L H, Zhang Y X, Liu Y, Chen X F. A new algorithm for electromigration failure analysis of metal interconnects [J]. ChineseJournal of Solid Mechanics, 2010, 31(2): 164-172(in Chinese).)
7 Liang L H, Zhang Y X, Chen X F, Liu Y. A new algorithm for EM analysis considering multiple driving forces mechanism [C].Proceedings of 10th Electronics Packaging Technology Conference, 2008:1137-1143.
8 Liu Y, Liang L H, Irving S, Luk T. 3D modeling of electromigration combined with thermal-mechanical effect for IC devices andpackage [J]. Microelectronics Reliability, 2008, 48(6): 811-824.
9 Reddy J N. An introduction to the finite element method [M]. 3rd ed. New York: McGraw-Hill, 2006.
10 Clement J J. Vacancy supersaturation model for electromigration failure under dc and pulsed dc stress. Journal of Applied Physics, 1992, 71(9):4264-4268.
11 Gee S, Kelkar N, Huang J, Tu K N. Lead-free and PbSn bump electromigration testing [C]. Proceedings of InterPACK 2005, 2005: 1-6.
12 Fan X J, Han Q. Design and Reliability in Wafer Level Packaging [C]. Proceedings of 10th Electronics Packaging Technology Conference, 2008: 834-841.
|


