论文导读::利用坐标变换的方法并结合保角映射技术,本文介绍了一种利用常规的各向同性材料来设计声波器件的方法。基于此理论,设计了二维声波隐身斗篷,并进行有限元模拟,证明了该器件的有效性,另外由于设计中没有利用材料共振的性质,所以器件是宽带有效的。该方法将有助于拓宽声波功能器件的设计,并为实验验证声波器件提供了可能。
论文关键词:保角坐标变换方法,声波器件设计,隐身斗篷
0 引言
声波传播和散射问题的深入研究是一个有趣的科学命题,蕴含着重要的应用背景。但是鉴于数学描述的复杂性,人们对于声波传播的认知还主要集中于均质和各向同性介质中。对于非均质、各向异性介质中波传播的特性,人们认知还比较少。不过真实世界中的介质往往是非均匀且各向异性的。在这样的条件下波的传播问题更加复杂,但也更加精彩隐身斗篷,因此值得深入的探讨。
如果说给定材料和几何边界的情况下去求解波场分布情况是一个正问题,那么根据给定外界波场反推材料属性和相关的几何边界情况就是一个波的反问题中国知网论文数据库。正问题的研究已经十分困难,反问题的研究则更具有挑战性,但这样的研究却是很有意义的,因为它解决的其实是一个波的控制问题。
本文中声波器件实际上就是一些经过精细设计的特殊波导结构;在结构外形和材料分布的控制下,以达到改变波的传播特性的目的。与传统的波导结构相比,它具有许多新的特点,对于波场的控制有了极大的灵活性,应用前景广泛。当前许多研究领域,都对电磁波和声波的控制问题给予了很高的重视,也取得了很大的进展隐身斗篷,追根溯源,除去新材料的发展,可以不夸张的说,一个很重要的原因在于所谓的坐标变换方法的运用。该方法由Pendry和Leonhardt [1,2]最先提出,
本文的设计也是基于此方法,再进行改进后得到的。针对电磁波的控制问题,Pendry等人提出的坐标变换方法的核心思想是利用Maxwell方程组在坐标变换下的形式不变性进行材料设计,近年来得到了许多有趣的电磁波控制器件,如电磁波平面透镜、弯波器、以及隐身斗篷等,其中一些器件逐渐被随后的实验所验证[3,4]。
实际上该方法并不仅仅限于电磁波,把它用于声波控制的研究也得到了越来越多的重视[5]隐身斗篷,这一研究分支被称为变换声学。但是根据目前的大多数变换声学方法所设计出声波器件都具有很强的各向异性的性质[6],例如要求动态质量密度为二阶张量形式等。为了达到这种要求往往需要在局部共振意义上进行动力学等效处理,这样不但使设计很难在工程中实现,而且也会受到工作带宽的限制。针对这样的问题,本文将介绍一种利用保角变换的方法来加以改进的思路,使最终的设计仅用通常的各向同性工程材料就可以实现,而且整个设计过程中没有局部共振的要求,从而可以实现宽带效果。
1 保角坐标变换方法
下面首先给出此问题的公式推导[7]。不同于已有理论,在公式推导中,没有假设材料参数为二阶张量形式,即认为所有材料参数仍保持为标量。标量形式的声波的控制方程为:
 (1) (1)
式中 是声波压力, 是声波压力,  为声介质密度, 为声介质密度,  为声介质体积模量中国知网论文数据库。对于任意给定的坐标变换 为声介质体积模量中国知网论文数据库。对于任意给定的坐标变换 隐身斗篷,将原空间的 隐身斗篷,将原空间的 坐标映射到像空间 坐标映射到像空间 中,同时要求 中,同时要求 ,可以证明方程(1)的左边将变成: ,可以证明方程(1)的左边将变成:
 ,(2) ,(2)
式中 。 。
在保角变换时,由于雅可比矩阵 可以表示为 可以表示为 ,其中 ,其中 是一个正的标量,而 是一个正的标量,而  是一个正交矩阵。再将 是一个正交矩阵。再将 代入方程(2),得到 代入方程(2),得到 。因此方程(1)可以表示为: 。因此方程(1)可以表示为:
 ,(3) ,(3)
式中  , ,  与 与 分别是 分别是 和 和 的标量缩放因子。 的标量缩放因子。
进一步考虑阻抗匹配的条件:
 (4) (4)
并要求公式(1)与(3)具有相同的表达形式,就可以得到最终器件设计所需的材料参数:
 , , (5) (5)
这样得到的器件完全可以通过使用通常的各向同性材料实现隐身斗篷,从而使得到的声学器件更加便于工程实现。
2 声波隐身斗篷实现
利用上节的理论公式,本节希望进行声学器件的设计。其中最具代表性的应该是隐身斗篷。它可以看作是目前电磁波隐身斗篷在声波领域的一个拓展。本文所给出的例子在文献[8]中曾被讨论过,其基本思路如图1所示:黄色梯形区域代表隐身区域,当入射波从左侧入射的时候,由于外部隐身器件(显示为灰色的区域)的作用,导致声波发生弯曲。根据精细设计的隐身斗篷会改变声波的传播路径,使其光滑地绕过隐身区域,之后在其前方又恢复成原来的路径,同时声波不会在隐身区域的后方发生反射。这样无论在隐身区域前方或者是后方进行声波探测,其所得的波场与隐身区域不存在时探测的情况将是一样的,从而最终实现了对区域隐身的目的。
遗憾的是隐身斗篷,由于Pendry所用方法的限制,如前面所说,其所需材料要具有较强的各向异性的性质,这给工程实现带来了很多困难。

图1 隐身斗篷示意图
Fig.1 Scheme of the tunnel cloak
为了说明本文方法的有效性,本文重新设计了该种隐身斗篷中国知网论文数据库。首先需要构造恰当的保角变换,这里采用的是Schwarz-Christoffel (S-C)变换。S-C变换是复变分析中常见的用于产生保角变换的方法,基本思路可以参见文献[9]。这里我们将图2(a)映射到图2(b),即将半平面映射为在线段 和射线 和射线 , ,  上的半平面。 上的半平面。

图2 利用S-C变换得到变换关系
Fig.2Construction of the transformation
这样可以直接得到映射方程:
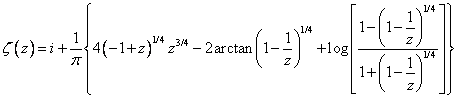
 , ,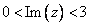 ,式中 ,式中 (6) (6)
从图2(b)不难发现,只要在此基础上将其沿轴 作镜像复制就可以得到最终的隐身斗篷。在已知斗篷的外部形式之后,通过公式(5)和(6),不难进一步得到其中材料分布的情况隐身斗篷,如图3所示。其中图3(a)为密度缩放因子 作镜像复制就可以得到最终的隐身斗篷。在已知斗篷的外部形式之后,通过公式(5)和(6),不难进一步得到其中材料分布的情况隐身斗篷,如图3所示。其中图3(a)为密度缩放因子 ,图3(b)为体积模量因子 ,图3(b)为体积模量因子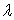 。 。
1/2 1 2 下一页 尾页 |


