由定义知 , , 满足 满足


因此判断因素T的影响是否显著等价于检验

判断因素B的影响是否显著等价于检验

对上述假设构造检验统计量采用离差平方和分解的方法,当不存在交互作用时,总离差平方和分解为三部分:温度因素T的平方和,场强因素B的平方和及随机因素的误差平方和。记为
 , ,
 , ,

将总离差平方和进行分解

 
其中


如果假设 与 与 是正确的,则所有的样本 是正确的,则所有的样本  ,可以看成来自同一正态总体 ,可以看成来自同一正态总体 ,根据定理: ,根据定理:
设总体U服从正态分布 霍尔电压,从总体U中抽取样本 霍尔电压,从总体U中抽取样本 , , ,…… ,…… ,样本均值和样本方差分别为 ,样本均值和样本方差分别为 和 和 ,则: ,则:
(1)
(2) 与 与 相互独立。 相互独立。
可知,

由于
 ~ ~ , ,
且

所以

由于 ~ ~ , ,
且 , ,
所以

此外,可以证明 , , , , 相互独立,并且 相互独立,并且

把 , , 及 及 分别除以相应的自由度,得到因素T,因素B及误差的平均离差平方和 分别除以相应的自由度,得到因素T,因素B及误差的平均离差平方和
 , , , ,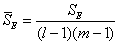
由F分布的定义可知
 , ,

当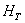 、 、 不为真时, 不为真时, , , 有偏大的趋势。于是对于给定的显著水平 ,查得临界值 有偏大的趋势。于是对于给定的显著水平 ,查得临界值

 , ,
当 时拒绝 时拒绝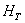 ,认为温度因素T的不同水平差异显著;当 ,认为温度因素T的不同水平差异显著;当
 时拒绝 时拒绝 ,认为因素B的不同水平差异显著;否则接受。 ,认为因素B的不同水平差异显著;否则接受。
四.总结
文章通过建立双因素方差分析模型对霍尔电压在一定温度和场强条件下的实验数据进行分析,判断温度因素和场强因素在一定条件下对霍尔电压是否有显著影响。双因素方差分析模型还可以应用到其它的物理实验中[5],如应用到考虑气流大小和气垫导轨的倾斜度对加速度的影响的牛顿第二定律验证的实验中。把双因素方差分析模型应用到物理实验中,判断实验条件中,哪些是主要影响因素,哪些是次要因素,判断两方面实验因素对实验结果是否有显著的影响很有帮助。
参考文献
[1]卢文科,朱长纯,方建安.霍尔元件与电子检测应用电路[M].北京:中国电力出版社,2005:112-119
[2]李学慧.大学物理实验[M].北京:高等教育出版社,2005:76-78
[3]邓远北,周润兰.应用概率统计[M].北京:科学出版社,2001:187-189
[4]张国权.应用概率统计[M].北京:科学出版社,2003:173-175
[5]王亚辉,王艳芬.方差分析在物理实验中的应用[J].宜宾学院学报,2009,9(6):30-31.
2/2 首页 上一页 1 2 |


