令 ，可得二阶金字塔点阵芯体结构沿1向的等效剪切模量 为：
3.2.3 2方向压缩等效弹性参数计算
当结构受2方向的压缩载荷时，单杆的受力如图7所示，其横截面如图8所示。杆件端点沿水平方向的约束反力为 ,两端弯矩分别为 。 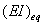， 分别为大杆横截面的等效抗弯刚度和等效抗轴向拉压刚度， 为 方向的厚度， 为垂直纸面 方向的杆的宽度。大杆受力相当于夹芯板的受力，则大杆的等效抗弯刚度 ， ，其中下标 和 分别指面板和芯材。此时，除了杆件端点沿外载荷方向的位移外其余位移均为根据杆件的平衡条件可得：
 
图7 2方向等效压缩时结构中一阶大杆件的边界条件及受力  
图82方向等效压缩时结构中一阶大杆件的横截面
按照一阶金字塔的推导方法，我们得到二阶金字塔中大杆两端的轴力和弯矩为
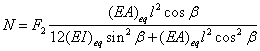
令 ，可得二阶金字塔点阵芯体结构沿2向的等效压缩模量 为：
4. 有限元模拟
在有限元中，我们用ABAQUS软件建立如图1中的一阶和二阶金字塔芯体单胞结构模型。大杆件与1、2、3（或是 ）三个方向的夹角分别为 宏观等效，二阶小杆与 三个方向的夹角分别为 。通过改变大杆和小杆的尺寸，我们得到六组不同相对密度的模型。大杆和小杆的具体尺寸见表1。假定杆件材料为理想弹塑性材料，其弹性模量 ，泊松比 ，屈服强度 。
表1 六组模型的具体尺寸
|
相对密度
|
结构
|
大杆
 mm
|
大杆单胞
 mm
|
二阶小杆 mm
|
小杆单胞 mm
|
|
0.0436
|
二阶
|
|
|
|
|
|
一阶
|
|
|
/
|
/
|
|
0.0254
|
二阶
|
|
|
|
|
|
一阶
|
|
|
/
|
/
|
|
0.01082
|
二阶
|
|
|
|
|
|
一阶
|
|
|
/
|
/
|
|
0.0062
|
二阶
|
|
|
|
|
|
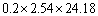
一阶
|
|
|
/
|
/
|
|
0.00378
|
二阶
|
|
|
|
|
|
一阶
|
|
|
/
|
/
|
|
0.000532
|
二阶
|
|
|
|
|
|
一阶
|
|
|
/
|
/
|
在模拟中，一阶和二阶芯体上下都是连接在两个刚体上，主要研究一阶芯体和二阶芯体的弹性参数。芯体杆件采用三维应力单元，载荷为位移加载在上面刚体的参考点上，下面刚体固定。这六组模型3方向等效压缩模量、1方向等效剪切模量及2方向等效剪切模量与结构相对密度之间的关系如图9所示。从图9 (a)、(b)、(c)三图可以看出，对于一阶和二阶金字塔芯体结构而言，其弹性模量和剪切模量的理论计算值与有限元模拟结果完全吻合，这也证明了本文理论计算的正确性。
 
图 9 一阶和二阶金字塔结构的宏观等效弹性参数与相对密度曲线：(a)等效压缩模量与相对密度曲
线，(b) 1方向等效剪切模量与相对密度曲线，(c)2方向等效剪切模量与相对密度曲线。
5. 结论
本文用理论推导和有限元研究了图1所示一阶金字塔芯体结构和二阶金字塔芯体结构的等效弹性参数。采用基于离散单元化方法给出材料的力学性能，理论计算了两种芯体结构的等效弹性常数。并利用ABAQUS分析软件对计算结果进行了验证。结合理论计算及有限元模拟结果可得出以下结论：本文的理论推导和有限元模拟结果相近。对于具有相同密度的一阶金字塔芯体结构和二阶金字塔芯体结构，其刚度近乎相同。
参考文献
[1]T. Bhat, T. Wang, L. Gibson, Micro-Sandwich Honeycomb, SAMPE J, 25 (1989).
[2]R. Lakes, Materials with structural hierarchy, Nature, 361 (1993) 511-515.
[3]G. Kooistra, V. Deshpande, H. Wadley, Hierarchical corrugated core sandwich panelconcepts, Journal of Applied Mechanics, 74 (2007) 259.
[4]陈爱萍，陈常青，卢天健。几种新型点阵材料等效参数和破坏模式的理论研究。中国力学学会学术大会论文摘要集（2009）。.
[5]H. Allen, Analysis and design of structural sandwich panels. 1969, in,Pergamon, New York.
3/3 首页 上一页 1 2 3 |
