由杆上端沿 方向上的位移为零和杆上端转角为零有：
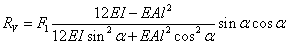
则杆件中的轴力为
用单位载荷法可以计算杆长为l的杆件位移对单胞沿1方向位移的贡献 为：
由单胞宏观应力和宏观应变在弹性范围内的关系
并令 ，可得一阶金字塔点阵芯体结构沿1向的等效剪切模量 为：
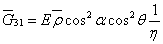
3.1.3 2方向剪切时等效弹性参数计算
当结构受2方向的压缩载荷时，单杆的受力如图4所示。杆件端点沿水平方向的约束反力为, 杆两端弯矩分别为 。 ， 论文开题报告。此时，除了杆件端点沿外载荷方向的位移外其余位移均为根据杆件的平衡条件可得：
 
图4 2方向等效压缩时结构杆件的边界条件及受力模型
由杆上端沿方向上的位移为零和杆上端转角为零有：
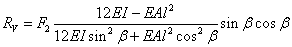
则杆件中的轴力为
用单位载荷法可以计算杆长为l的杆件位移对单胞沿2向位移的贡献 为：
由单胞宏观应力和宏观应变在弹性范围内的关系
并令 ，可得一阶金字塔点阵芯体结构沿2向的等效压缩模量 为：
3.2 芯体压缩等效弹性参数计算
3.2.1 3方向压缩等效弹性参数计算
当结构受3方向的压缩载荷时，单杆的受力如图2b所示，其横截面如图5所示。杆件端点沿水平方向的约束反力为 , 杆两端弯矩分别为。 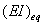， 分别为大杆横截面的等效抗弯刚度和等效抗轴向拉压刚度， 为 方向的厚度， 为垂直纸面 方向的杆的宽度。大杆受力相当于夹芯板的受力宏观等效，则大杆等效抗弯刚度 ， [5]，其中下标 和 分别指面板和芯材。此时，除了杆件端点沿外载荷方向的位移外其余位移均为根据杆件的平衡条件可得：
 
图5 3方向等效压缩时结构中一阶大杆件的横截面
按照一阶的推导方法，我们可以得到二阶芯体大杆中的轴力和弯矩分别为
令 ，可得二阶金字塔点阵芯体结构沿3方向的等效压缩模量 为：
3.2.2 1方向压缩等效弹性参数计算
当结构受1方向的压缩载荷时，单杆的受力如图6所示，其横截面如图5所示。杆件端点沿水平方向的约束反力为, 两端弯矩分别为。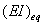，分别为大杆横截面的等效抗弯刚度和等效抗轴向拉压刚度，为方向的厚度，为垂直纸面方向的杆的宽度。大杆受力相当于夹芯板的受力，则大杆等效抗弯刚度 ，[5]，其中下标和分别指面板和芯材。此时，除了杆件端点沿外载荷方向的位移外其余位移均为根据杆件的平衡条件可得：
 
图6 1方向等效压缩时结构中一阶大杆件的边界条件及受力模型
按照一阶金字塔的推导方法，我们可以得到二阶芯体大杆中的轴力和弯矩分别为
2/3 首页 上一页 1 2 3 下一页 尾页 |
