本文研究了一类四阶非线性Schrödinger方程初边值问题在任意维空间中的 有界性,其结果在研究整体解时是非常重要的。 有界性,其结果在研究整体解时是非常重要的。
论文关键词:四阶,非线性Schrödinger方程, ,有界性 ,有界性
我们考虑这样一类非线性Schrödinger方程的初边值问题
 , ,  , (1.1) , (1.1)
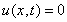 , ,  , (1.2) , (1.2)
 , ,  , (1.3) , (1.3)
其中, 为复值函数, 为复值函数, &,&为速降函数空间, &,&为速降函数空间, , ,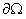 充分光滑, 充分光滑, 为实数。 为实数。
方程(1.1)-(1.3)具有特定的物理背景,且在数学理论上是一类非线性发展方程,因此对方程(1.1)-(1.3)的研究具有实际意义和理论意义。
为了研究方程(1.1)-(1.3)整体解的存在唯一性,需要解在 空间中的有界性质作为前提。 空间中的有界性质作为前提。 时,文[1~5]研究了方程(1.1)-(1.3)整体解的存在唯一性及渐近性质,文[6~7]讨论了方程(1.1)-(1.3)解的 时,文[1~5]研究了方程(1.1)-(1.3)整体解的存在唯一性及渐近性质,文[6~7]讨论了方程(1.1)-(1.3)解的 有界性。 有界性。 时,关于方程(1.1)-(1.3)解的 时,关于方程(1.1)-(1.3)解的 有界性的研究,就作者所知还是较少的。本文就 有界性的研究,就作者所知还是较少的。本文就 时给定初值一定要求前提下,用文[7]的方法得到了方程(1.1)-(1.3)解的 时给定初值一定要求前提下,用文[7]的方法得到了方程(1.1)-(1.3)解的 有界性。 有界性。
记号:简记 ,一切常数除注明者外,均以 ,一切常数除注明者外,均以 表示,且与 表示,且与 、 、 无关,且不同地方出现的 无关,且不同地方出现的 值可能不同,但为了方便,我们仍以 值可能不同,但为了方便,我们仍以 记之,其余记号都是标准的。 记之,其余记号都是标准的。
2 引理
因在奇维空间中的情形证明过程类似于偶维空间,我们不妨先讨论偶维情况。
引理1 对任意复值函数 , , ,如果 ,如果
 (2.1) (2.1)
那么有
 。 (2.2) 。 (2.2)
引理2 设 为正的可积函数, 为正的可积函数, 为有界区域,则存在只与 为有界区域,则存在只与 有关的常数 有关的常数 ,使得 ,使得
 (2.3) (2.3)
成立,其中 。 。
引理3[7] 设 ,如果 ,如果
 (2.4) (2.4)
那么有
 (2.5) (2.5)
证明 根据复合函数求导法则,知
 (2.6) (2.6)
其中
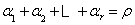

可算出





在 中每一项对 中每一项对 求导的阶数与求导因子次数之和等于 求导的阶数与求导因子次数之和等于 ,并且各导数因子的次数最大为 ,并且各导数因子的次数最大为 ,我们将 ,我们将 展开,注意到,展开式中的各项具有下列乘积形式: 展开,注意到,展开式中的各项具有下列乘积形式:
 (2.7) (2.7)
其中, 分别取自 分别取自 的表达式中的某一项,在 的表达式中的某一项,在 中的因子的最大个数是1,2,…,r。整理(2.7)式,其形式是 中的因子的最大个数是1,2,…,r。整理(2.7)式,其形式是
 (2.8) (2.8)
可以得知

即

令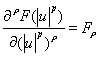 ,考虑(2.8)式,则(2.6)式化为 ,考虑(2.8)式,则(2.6)式化为

由假设知, ( ( 为与 为与 无关的常数),因此 无关的常数),因此

则有

由赫尔特不等式,得
 (2.9) (2.9)
由(2.4)式可知,(2.9)式的右端为与 无关的常数,因此有 无关的常数,因此有

根据引理2,有

因此, 。 。
3 主要结论
定理 如果 有界,并且 有界,并且
  ; ;
 
那么,方程⑴的解 满足 满足
 (3.1) (3.1)
证明 对(1.1)式两端同时作用 ,设 ,设 ,有 ,有
 (3.2) (3.2)
即
 (3.3) (3.3)
对(3.3)式两端同时乘以 ,并且在 ,并且在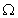 上对 上对 积分,得 积分,得

用分部积分法,得
 (3.4) (3.4)
取(3.4)式共轭,得
 (3.5) (3.5)
(3.4)式加上(3.5)式,可得

也即
 (3.6) (3.6)
对于 ,记 ,记 ,则 ,则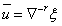 , , , ,

 (3.7) (3.7)
类似地,对 ,有 ,有
 (3.8) (3.8)
将(3.7)式,(3.8)式代入(3.6)式,得

在 上积分,得 上积分,得
 (3.9) (3.9)
其中, 为常数。(3.9)式可写成 为常数。(3.9)式可写成

 (3.10) (3.10)
从(3.10)式看出,右端 和 和 是类似的,只须证 是类似的,只须证 有界。 有界。
由于
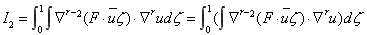 (3.11) (3.11)
只须证

中有界的,其中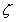 是 是 上的实参数。 上的实参数。
1/2 1 2 下一页 尾页 |


