 ( ( + + - - ) )
在上述基础上增加交易费用 ,得: ,得:
 (4) (4)
为使投资组合 在[ 在[ ]内仍是无风险的,就要调整投资策略。因保值调整策略而产生的交易份额差 ]内仍是无风险的,就要调整投资策略。因保值调整策略而产生的交易份额差 为: 为:
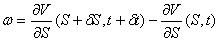 (5) (5)
利用Taylor定理, 将(5)式的第1项展开得:
 (6) (6)
又 ,忽略上式中关于 ,忽略上式中关于 的高阶无穷小项,有: 的高阶无穷小项,有:

由E( ) = ) = ,可得到交易成本 ,可得到交易成本 的数学期望: 的数学期望:

从而可得到 的数学期望: 的数学期望:

两边同时消去 并移项,可得有交易成本和支付连续红利情况下期权定价的B-S方程: 并移项,可得有交易成本和支付连续红利情况下期权定价的B-S方程:
 (7) (7)
二、求修正后B-S方程的看涨-看跌期权定价公式
用偏微分的知识来求解公式比较繁琐,我们可以根据Black-Scholes模型的公式来推广有交易费用和连续支付红利的情况论文网。将此股票与一只不支付红利的相似股票进行比较,红利的支付使得股票价格降低了等于红利的数量,所以支付连续红利率 使得股票价格的增长率比不支付时减少了 使得股票价格的增长率比不支付时减少了 。 。
令 ,带入(7)式中,考虑到: ,带入(7)式中,考虑到:

整理后,可得:

即 
令 数学建模论文, 那么有交易费用和红利的期权定价模型为: 数学建模论文, 那么有交易费用和红利的期权定价模型为:

而B-S基本模型为:

与有交易费用和红利的定价模型只差在无风险利率 上,所以,在B-S定价公式中,用 上,所以,在B-S定价公式中,用 代替 代替 即可得到有交易费用和红利的期权定价公式。 即可得到有交易费用和红利的期权定价公式。
有交易费用和红利的期权定价公式为:


其中, , ,
要求空头的期权定价公式,只要把
 改为 改为 即可。 即可。
三、添加交易费用和连续红利的期权定价公式的应用研究
本文选取了两个具有代表性的权证实例,马钢权证和云化权证。研究马钢权证在2006-11-29至2008-11-28这个时间段内和云化权证在2007-3-8至2009-3-7这个时间段内的B-S理论价格与修正价格的差异,进而说明交易费用和连续红利对期权价格的影响。
表1 马钢权证和云化权证的有关数据
|
权证代码
|
权证名称
|
起始日期
|
到期日期
|
行权价
|
|
580010
|
马钢CWB1
|
2006-11-29
|
2008-11-28
|
3.26
|
|
580012
|
云化CWB1
|
2007-3-8
|
2009-3-7
|
17.83
|
|
股票价
|
当日权证价
|
交易费比例
|
分红率
|
无风险利率
|
|
4.43
|
1.679
|
0.003
|
0.046
|
0.0252
|
|
22.62
|
9.34
|
0.003
|
0.018
|
0.0252
|
1 求隐含波动率
(1)马钢权证
到期日为 ,执行价格为 ,执行价格为 的B-S定价公式为: 的B-S定价公式为:



由表1可得,
通过MATLAB编程,可得马钢权证的隐含波动率为0.5136.
(2) 云化权证
到期日为 ,执行价格为 ,执行价格为 的B-S定价公式为: 的B-S定价公式为:



由表1可得,
通过MATLAB编程,可得云化权证的隐含波动率为0.6543.
2 B-S理论价格
(1) 马钢权证
由上所述,马钢权证的波动率为0.5136,则通过MATLAB编程有

查表有: =0.956, =0.956, =0.836 =0.836
则马钢权证的B-S理论价格为1.6437.
(2) 云化权证
云化权证的波动率为0.6543,令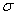 = =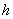 , , ,则可得 ,则可得
查表有: =0.9384, =0.9384, =0.7295 =0.7295
则云化权证的B-S理论价格为8.8589.
3 考虑交易费用和连续红利情况下的权证价格
(1) 马钢权证
有交易费用和支付红利时的期权定价公式为:

 , , , ,
2/3 首页 上一页 1 2 3 下一页 尾页 |


