论文导读::本文在经典B-S模型的基础上引入了交易费用和连续支付的红利,对期权定价公式进行了进一步研究,并且给出了存在交易费用和连续红利时的期权定价公式。通过马钢权证和云化权证的实例分析,进一步说明了有交易费用和连续红利存在时对期权价格的影响,并对结果进行了简要的分析。
论文关键词:B-S定价模型,交易费用,连续红利
期权是20世纪70年代中期在美国出现的一种金融创新工具,30多年来,它作为一种防范风险和投机的有效手段而得到迅猛发展。
1973年,美国芝加哥大学教授Black.F和斯坦福大学教授Scholes.M发表了一篇名为《The pricing of options and Corporate Liabilities》的著名论文,文章给出了Black - Scholes期权定价模型(以后简称B-S模型) ,推导出基于股票的任何一种衍生证券的价格必须满足的微分方程,并成功地求解该方程,因此获得诺贝尔经济学奖。该理论及其以后的多种变形,极大地推动了金融衍生工具市场的发展。
但经典的Black-Scholes模型在研究过程中忽略了交易费用和连续红利的存在,这样的模型在现实的金融市场中的实用性降低。为了更符合实际的金融市场,本文在Black-Scholes模型的基础上,引入了交易费用和连续红利,并且给出了存在交易费用和连续红利情况下的期权定价公式。然后又引进了两个实际的具有代表性的权证,进一步研究分析数学建模论文,说明交易费用和连续红利的存在对期权价格有影响论文网。
一、B-S模型及其修正模型
B-S基本模型为:

相应的看涨期权定价公式为:

看跌期权定价公式为:

其中:



这里 为期权价格, 为期权价格, , , 为原生资产价格(这里指股票价格), 为原生资产价格(这里指股票价格), 为期权敲定价格(执行价), 为期权敲定价格(执行价), 为到期日, 为到期日, 为当前时刻, 为当前时刻, 为预期收益率, 为预期收益率,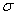 为波动率, 为波动率, 为无风险利率, 为无风险利率, 为标准Brown运动。 为标准Brown运动。
在实际交易中,股票的投资者通常会得到一定的股票红利,股票红利的支付有两种情况,每年在规定时间支付或者按照一定比例连续支付红利。本文只讨论连续支付的情况。前者可将除权日所支付的红利均摊到每一天,这样就可视为红利是连续支付的。在实际的金融市场中交易费用是非零的,而且对投资组合的权重进行连续调整会引起交易成本不断增加,所以在修改模型时有必要将交易成本也考虑在内。B-S方程是在连续条件下推导出来的,先在 时间内对期权套期保值,再令 时间内对期权套期保值,再令 → 0。但是,当存在交易费用时,就不能无限次地进行保值,否则交易费用也会达到无穷。因此,要适当修改基本假设里的部分条件,对基本假设做如下推广: → 0。但是,当存在交易费用时,就不能无限次地进行保值,否则交易费用也会达到无穷。因此,要适当修改基本假设里的部分条件,对基本假设做如下推广:
(1) 股票的价格适合随机微分方程以离散形式给出:
 (1) (1)
其中, 是服从标准正态分布的随机变量,其概率密度函数为: 是服从标准正态分布的随机变量,其概率密度函数为:

这里 不再是无穷小量,不再求趋于0 的极限 不再是无穷小量,不再求趋于0 的极限
(2) 无风险利率
(3) 股票连续支付股息(红利),红利率为
(4) 交易成本可看作是投资者因买卖股票而产生的直接费用,一般由买方支付, 并以交易额的固定比例M来表示。设交易ω股价格为S的股票数学建模论文,则交易费用为 (买为 (买为 ,卖为 ,卖为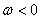 )。我们知道 )。我们知道 ,利用伊藤公式有: ,利用伊藤公式有:
 (2) (2)
利用 -对冲形成投资组合: -对冲形成投资组合:

要求选取适当的 ,使 ,使 在[ 在[ ]内无风险。设在时刻 ]内无风险。设在时刻 形成投资组合 形成投资组合 ,并在[ ,并在[ ]内,不改变份额 ]内,不改变份额 ,由于 ,由于 是无风险的,就有: 是无风险的,就有:


所以

考虑支付股息的情况,因为股息是无风险的收入,所以可与股票的平均收益率合并。股票持有者在 时段内的连续红利收益为 时段内的连续红利收益为 ,那么 ,那么
 (3) (3)
将(1)式和(2)式代入(3)式,得:
 由 由 ,得到等式 ,得到等式
 该等式右端是无风险的,因此等式左端的随机项 该等式右端是无风险的,因此等式左端的随机项 的系数必为0,于是 的系数必为0,于是
 ,则 ,则 的表达式可简化为: 的表达式可简化为:
1/3 1 2 3 下一页 尾页 |


