点为数集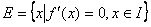 孤立点(定义见文献3)开区间,则函数 孤立点(定义见文献3)开区间,则函数 在区间 在区间 上严格增加 上严格增加
(严格减少).注:事实上只须将任意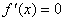 相邻两点分别使用定理2的方法便可得到. 相邻两点分别使用定理2的方法便可得到.
定理3.(最值定理)若函数 在闭区间 在闭区间 上连续,则 上连续,则 在 在 必取得最大值( 必取得最大值( )与最小值( )与最小值( ). ).
定理4.(积分中值定理)  若函数 若函数 在闭区间 在闭区间 上连续,则至少存在一点 上连续,则至少存在一点  使得式子 使得式子 成立. 成立.
证明:因为函数 在闭区间 在闭区间 上连续,由定理3可得 上连续,由定理3可得 在 在 必取得最大值( 必取得最大值( )与最小值( )与最小值( ).由定积分的性质(见文献5)可得 ).由定积分的性质(见文献5)可得

故有

依据闭区间上连续函数的介值定理,在闭区间 上至少存在一点 上至少存在一点 ,使得 ,使得
   . .
因此有
   . .
2.定理(条件加强)及应用
定理5.(积分中值定理)若函数 在闭区间 在闭区间 上连续且严格单调,则至少存在一点 上连续且严格单调,则至少存在一点  使得式子 使得式子 成立. 成立.

图1-1
证明:不妨假设 严格递减(如图1-1所示)显然有 严格递减(如图1-1所示)显然有

即
 (ⅰ) (ⅰ)
由定理4可得至少存在一点  使得 使得
 成立. (ⅱ) 成立. (ⅱ)
将(ⅱ)代入(ⅰ)得到
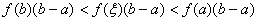 (ⅲ) (ⅲ)
三边同处除 得到 得到
 (ⅳ) (ⅳ)
又因为 严格递减开区间,所以有 严格递减开区间,所以有

即 属于开区间 属于开区间 ,定理5得证. ,定理5得证.
例1证明
证明 由积分中值定理4可得
 
两边取极限得
  =0 ( =0 ( , , ) )
在例1中 ,或 ,或 均有 均有 成立,并未影响结论下面我们再看一个例子. 成立,并未影响结论下面我们再看一个例子.
例2证明
分析:因为被积函数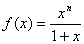 ,由积分中值定理4可得至少存在一点 ,由积分中值定理4可得至少存在一点 属于闭区间 属于闭区间 使得 使得 成立,而 成立,而 该证明方法失败开区间,其原因 该证明方法失败开区间,其原因 取到了闭区间的右端点1,下面我们给出正确的证法. 取到了闭区间的右端点1,下面我们给出正确的证法.
证明: 因为被积函数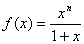 在 在 可导. 可导.
对 , ,
由定理2可得 在 在 严格递增,由定理5可得存在一点 严格递增,由定理5可得存在一点 使得 使得
 
两边取极限得
  =0 =0
3结语
1 在原有的积分中值定理中加强了被积函数的条件得出了至少存在一点 在原有的积分中值定理中加强了被积函数的条件得出了至少存在一点 属于开区间 属于开区间 的结论. 的结论.
2 就例2而言还有更简单的办法比如放缩法,而积分中值定理方法更具一般性. 就例2而言还有更简单的办法比如放缩法,而积分中值定理方法更具一般性.
此外,我们还证出了函数 在区间 在区间 上严格增加(严格减少)更一般的结论(定理2的推论). 上严格增加(严格减少)更一般的结论(定理2的推论).
参考文献
[1]刘玉链,傅沛仁.数学分析讲义[M]. 北京:高等教育出版社,1985. 15-16;237.
[2]同济大学应用数学系编.高等数学(上册)[M] 北京:高等教育出版社,2002. 127-128
[3]华东师范大学数学系编.数学分析(下册)[M]. 北京:高等教育出版社,1987. 113
[4]?咏生,刘洪运,刘庆芝?.高等数学[M]. 西安:西北工业大学出版社,2008.42-43
[5]李心灿.高等数学[M]. 北京:高等教育出版社,2003.160-161
2/2 首页 上一页 1 2 |


