| (3)为了提高系统集成架构、敏捷重构和安全能力,同时协同各种类型客户端进行工作,必须开发一个功能完备、采用分层体系模式的信息集成系统。
综上所述可知,时间压缩和信息交互系统的建立是实现IC供应链的关键。以下本文针对时间压缩问题进行研究。
4.时间压缩
时间作为一种战略武器,与资本、生产率、质量、甚至创新同等重要,供应链竞争优势在于以更低的价格、更快的速度给顾客提供更多的价值。因此对供应链时间的研究成为广大学者关注的重点。
4.1供应链时间的研究现状
目前,有大量文献研究供应链中的时间问题,但是存在着以下问题:
(1)只涉及供应链的局部作业环节时间的研究,如采购时间、内向运输时间、外向运输时间、设计时间、制造时间、分销时间;
(2)虽然已有文献在建立关于供应链管理的数学模型时,考虑了时间因素,但是绝大多数只是作为数学模型的一个约束条件,研究主要围绕成本进行。
(3)有些文献虽然研究了供应链中的时间,但只是建立时间因素的数学模型,并没有进行深入研究。
4.2供应链总周期时间
通常所研究的基于某个节点企业单一环节(如产品生产周期)的快速响应是没有实际意义的,必须从整个生产和物流过程出发研究响应周期的问题,这样才能真正提高某种产品的供应链在最终用户市场上的竞争力。基于此,马士华教授(2001)年提出了供应链多阶响应周期(Multi-stageResponseTimeinSupplyChain)概念,多阶响应周期就是由供应链上不同阶段的子周期所构成的全供应链的周期。

图2供应链多阶响应周期
如图2所示,IC供应链总周期时间是指整个IC供应链为满足顾客需求花费的总时间,它由五大时间构成要素组成:订单处理周期、产品设计周期、采购/供应周期、生产/装配周期和物流周期。
5.供应链响应时间的关键构成要素分析
供应链作为一个系统,整体优化往往只取决于极少数的环节,即薄弱环节。我们借用生产管理中的约束理论(TOC)对供应链进行薄弱环节分析。从TOC的角度看,供应链上的活动可以分为两类:“瓶颈”和“非瓶颈”。整个供应链的响应时间是由瓶颈决定的,所以要缩短整个供应链的响应时间,必须把精力集中放在瓶颈上,尽可能提升其能力,减少其转换次数和转换时间。一旦识别出瓶颈,就应将关键的资源配置到瓶颈环节中,提高其批量,减少其转换次数,保持各非瓶颈环节与瓶颈环节同步运行,从而达到缩短供应链总周期时间的目的。然而,如何找到“瓶颈”呢?本文采用灰关联分析法寻找影响供应链时间的“瓶颈”。
灰关联分析法是邓聚龙于1989年提出的,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。灰色关联度不光考虑了比较数列在数值上对参数列的贡献程度,更为重要的是它动态地看问题,从各比较数列的发展态势上作比较分析。
根据图2所示的供应链总周期时间的要素组成,将它们用表1的符号表示:
表1时间构成要素的表示符号
|
序号
|
时间构成要素
|
符号
|
|
0
|
供应链总周期时间
|

|
|
1
|
订单处理周期
|

|
|
2
|
产品设计周期
|

|
|
3
|
采购/供应周期
|

|
|
4
|
生产加工周期
|

|
|
5
|
物流周期
|

|
设原始序列 为非平滑序列,作为参考系列,它是指供应链总周期时间组成的序列;设原始序列 为非平滑序列,作为参考系列,它是指供应链总周期时间组成的序列;设原始序列 也均为非平滑序列,作为比较系列,他们分别是指订单处理周期、产品设计周期、采购/供应周期、生产加工周期和物流周期组成的序列,如表5-1所示。 也均为非平滑序列,作为比较系列,他们分别是指订单处理周期、产品设计周期、采购/供应周期、生产加工周期和物流周期组成的序列,如表5-1所示。
灰关联分析的步骤如下:
①原始数据的无量纲分析
对系统行为作量化研究分析,需要对各构成要素进行适当处理。通过初值化作用,使之化为数量级相当的无量纲数据。初值化是指所有数据均用第一个数据去除,然后得到一个新的序列 , , 。 。 的计算公式如下: 的计算公式如下:
 (1) (1)
这个新的序列形成如下矩阵:
 (2) (2)
②计算差序列、最大差和最小差
求差序列的计算公式如下:算公式如下:
 (3) (3)
式中: , , 。同时,形成如下绝对差值矩阵: 。同时,形成如下绝对差值矩阵:
 (4) (4)
最小数即为最大差和最小差:
 , , (5) (5)
③计算灰关联系数
灰关联系数 的计算公式如下: 的计算公式如下: (6) (6)
式中 , , 。 。 是分辨系数, 是分辨系数, 是在(0,1)中取定得实数,它的值通常取0.5。 是在(0,1)中取定得实数,它的值通常取0.5。
灰关联系数 是指比较序列对参考序列在 是指比较序列对参考序列在 点的关联水平。由 点的关联水平。由 可以得到关联系数矩阵: 可以得到关联系数矩阵:
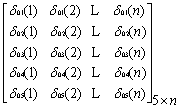 (7) (7)
④计算灰关联度
灰关联度 计算的一般表达式是: 计算的一般表达式是:
 (8) (8)
式中 , , 。 。
最后,依关联度进行排序,关联度大的即为影响供应链总周期时间大的构成要素,是供应链时间管理中最值得关注的焦点。
6.结论
本文针对与即时顾客化定制(IC)这一全新的生产模式的供应链管理方法展开了研究。 2/3 首页 上一页 1 2 3 下一页 尾页 |


