= 
通过前文的分析,结合问题特点,作如下假设:
1)各项训练任务对主要资源的占用无先后顺序。
2)同一项训练任务对主要资源的使用无先后顺序。
3)各项训练任务对循环使用型资源的使用是可中断的。
根据以上假设,即可将上述问题转化为排序问题:

记 ,有 ,有 。 。
对应于 的时间表长度下界为 的时间表长度下界为 。 。
定义1:若 的某行(列)全部元素之和等于下界 的某行(列)全部元素之和等于下界 ,则称此行(列)为紧行(列),否则称为松行(列)。 ,则称此行(列)为紧行(列),否则称为松行(列)。
定义2:对于矩阵 定义减量集 定义减量集 如下: 如下: 是 是 的一个非零元素子集。对 的一个非零元素子集。对 的每个紧行,每个紧列, 的每个紧行,每个紧列, 恰好含有其中一个元素,而对 恰好含有其中一个元素,而对 的松行和松列, 的松行和松列, 中至多含有其一个元素。 中至多含有其一个元素。
对于任何一个非负矩阵(矩阵中元素均不小于 )必存在一个减量集。利用减量集 )必存在一个减量集。利用减量集 ,可以构造一个长度 ,可以构造一个长度 经过适当选择的部分排序表,在这个部分排序中,对减量集中的每个元素 经过适当选择的部分排序表,在这个部分排序中,对减量集中的每个元素 ,第 ,第 类主要循环使用资源被训练任务 类主要循环使用资源被训练任务 占用的时间为 占用的时间为 个单位时间。 个单位时间。
在原始的训练任务/主要循环使用资源时间占用矩阵 中,对于减量集中的元素减少到 中,对于减量集中的元素减少到 ,从而得到新的训练任务/主要循环使用资源时间占用矩阵 ,从而得到新的训练任务/主要循环使用资源时间占用矩阵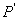 。如果 。如果 适当选择,对应于 适当选择,对应于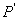 的时间表长下界为 的时间表长下界为 。 。
 的选择须满足下列条件: 的选择须满足下列条件:
不能大于减量集 中属于紧行紧列的每个元素 中属于紧行紧列的每个元素 ,否则在 ,否则在 转化为 转化为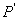 的过程中,紧行紧列元素和减少量可能少于 的过程中,紧行紧列元素和减少量可能少于 , ,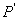 中将有某行某列,其元素和严格大于 中将有某行某列,其元素和严格大于 。 。
若 是松行(第 是松行(第 列)的元素,为使对应于 列)的元素,为使对应于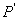 的时间表长度为 的时间表长度为 ,则应有 ,则应有 。 。
同理,若 是松列(第 是松列(第 行)的元素,则 行)的元素,则 。 。
若第 行中不含减量集中的元素,为使对应于 行中不含减量集中的元素,为使对应于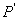 的时间表长度为 的时间表长度为 ,则应有 ,则应有 ,即 ,即 。 。
同理,若第 列中不含减量集中的元素,则 列中不含减量集中的元素,则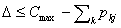 。 。
上述限制是为使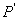 对应的时间表长不超过 对应的时间表长不超过 。 。
在满足上述限制下,尽可能大的选择 ,则或者 ,则或者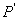 比 比 至少一个正元素,或者, 至少一个正元素,或者,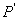 比 比 至少多一个紧行或紧列。 至少多一个紧行或紧列。
上述过程不超过 次重复( 次重复( 是原始时间占用矩阵 是原始时间占用矩阵 中正元素的个数),可得到一系列部分排序,最后组成整体最优排序。 中正元素的个数),可得到一系列部分排序,最后组成整体最优排序。
算法:
a)设当前时刻,训练任务/主要循环使用资源时间占用矩阵为 ; ;
b)求减量集 ,确定部分排序; ,确定部分排序;
c)确定新的训练任务/主要循环使用资源时间占用矩阵;
d)若由新训练任务/主要循环使用资源时间占用矩阵可以直接得到排序表,则停止,否则转a)。
3.2装备保障训练资源需求计算
具体求解步骤如下:
1)在现有装备保障训练资源的使用优化求解的基础上,判断 与 与 的关系。 的关系。
2)若   ,只需计算附属循环使用型资源、消耗型资源及相应教学人员的投入即可。转步骤六。 ,只需计算附属循环使用型资源、消耗型资源及相应教学人员的投入即可。转步骤六。
3)若 > > ,此时认为人员训练的总时间、各批次训练时间都为定值,训练的进程——即对资源的使用顺序,已进行了合理的安排,并达到最优。此时,需增加主要资源,使总的训练时间缩短。转入下一步。 ,此时认为人员训练的总时间、各批次训练时间都为定值,训练的进程——即对资源的使用顺序,已进行了合理的安排,并达到最优。此时,需增加主要资源,使总的训练时间缩短。转入下一步。
4)计算所需追加的主要资源数量。根据各批次的第 训练任务对第 训练任务对第 类主要循环使用资源的总占用时间 类主要循环使用资源的总占用时间 ,在所需训练时间 ,在所需训练时间 内所占的比例,计算追加资源后各批次第 内所占的比例,计算追加资源后各批次第 训练任务对第 训练任务对第 类主要循环使用资源实际所需占用的时间 类主要循环使用资源实际所需占用的时间 ,再根据 ,再根据 计算追加的主要资源数量。 计算追加的主要资源数量。
 / / = = / /
 = =

 —实际所需第 —实际所需第 种主要资源数量; 种主要资源数量; —所需追加第 —所需追加第 种主要资源数量。 种主要资源数量。
5)步骤五:计算追加的主要资源的费用。
 = =
 —追加主要资源的费用; —追加主要资源的费用; —追加的主要资源的单位成本。 —追加的主要资源的单位成本。
6)计算追加的附属资源数量、费用。按照各门课程同时进行的数量统计所需各类附属资源,对比现有资源进行添加,并计算追加费用。
 
 —追加附属资源的费用; —追加附属资源的费用; —所需追加第 —所需追加第 种附属资源数量; 种附属资源数量; —第 —第 种附属资源单位成本。 种附属资源单位成本。
7)计算教学人员的数量。按照各门课程同时所进行的最多班数,计算教员的需求数量。 2/3 首页 上一页 1 2 3 下一页 尾页 |


