论文导读::本文在概述层次分析法的基本原理的基础上,针对现有产品方案选择方法的缺陷,探讨了层次分析法在产品方案选择中的应用问题,希望对企业的此类问题有所帮助。
论文关键词:层次分析法,方案选择,应用
一、问题的提出
企业为了增强产品的市场竞争力,吸引顾客,必须提高其产品作为商品的价值。为此,要对产品各原理方案进行分析评价,新产品方案的选择评价是一个群体决策问题,其决策思路是先分别求出每一个方案的所有决策者的偏好意见的集结值,然后对其排序进行决策。在国内的研究中,产品方案选择的方法一般有直接评分法和确定方案系数评价法等,这些方法在一定程度上能够对事物进行量化且有一定的科学性, 但也存在着一些缺陷。层次分析法是为解决复杂问题评价而产生的,它采用定量与定性相结合的分析方法, 适合于解决产品方案选择等量化和评价问题上。
二、层次分析法的基本原理
层次分析法(AnalyticHierarchy Process,简称AHP)是美国运筹学家T.L.Saaty于上个世纪70年代提出的一种在处理复杂的决策问题中,进行方案比较排序的方法,其核心思想是把复杂的决策问题层次化,把决策问题按总目标、子目标、评价标准、直到具体措施的顺序分解为不同层次的结构;上一层元素对相邻的下一层次的全部或部分元素起支配作用;然后利用求判断矩阵的特征向量办法企业管理论文,求得每一层的各元素对上一层次某元素的权重,然后通过加权和的方法递阶归并,求出最低层(供选择的方案或具体措施)、最高层(总目标)的相对重要性,从而对最低层各元素进行优劣等级的排序。
1、构造出层次结构模型各层次的判断矩阵
依据AHP原理和程序,聘请有关专家,自上而下对产品各构成部件指标进行两两重要程度判断比较,构造判断矩阵 。为了使因素之间进行两两比较,得到量化的判断矩阵,根据心理学家的研究提出:人们区分信息等级的极限能力为7±2,引入1~9的标度,如表1所示。根据标度表构造产品各构成部件各层级指标的两两判断矩阵如表2所示: 。为了使因素之间进行两两比较,得到量化的判断矩阵,根据心理学家的研究提出:人们区分信息等级的极限能力为7±2,引入1~9的标度,如表1所示。根据标度表构造产品各构成部件各层级指标的两两判断矩阵如表2所示:
表1 标度值表表2 层次分析法中两两比较判断矩阵
|
标度
|
定 义
|
|
1
|
i因素与j因素同样重要
|
|
3
|
i因素比j因素略重要
|
|
5
|
i因素比j因素较重要
|
|
7
|
i因素比j因素非常重要
|
|
9
|
i因素比j因素绝对重要
|
|
2、4、6、8
|
为以上两种判断之间的中间状态对应的标度值
|
|
倒数
|
j因素比较i因素得到的判断值为
|
2、根据判断矩阵依次计算下列各项:
(1) 
(2) 
(3) 对向量 归一化, 归一化,  得 得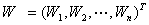 即为权重向量。 即为权重向量。
(4) 计算判断矩阵 最大特征根 最大特征根


(5) 一致性检验
CI=
RI由表3查得,得CR=CI/RI。若CR<0.1,则认为排序结果有满意的一致性,如未能通过一致性检验,则需要重新调整矩阵元素直至通过检验中国知网论文数据库。
表3 修正值RI
|
标度
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
RI
|
0.00
|
0.00
|
0.58
|
0.90
|
1.12
|
1.24
|
1.32
|
1.41
|
1.45
|
1.49
|
三、层次分析法在产品方案选择上的应用
方案评价的科学性关系到方案选择的正确性。通过利用层次分析法对备选方案进行评价, 将克服价值工程中传统定量分析方法缺乏一致性检验的缺点,做出更为科学的判断。假设企业总目标是选择某产品的设计方案,以实现降低成本,维持企业的持续竞争能力。根据企业的总目标分析,可采取以下三个准则来评价备选方案是否合理。其主要评价因素分别是成本B1、功能B2、外观B3,为了实现这三项子目标,有四个可供选择,分别是方案C1、方案C2、方案C3与方案C4。
 (一)构建其层次结构模型如图1 所示。 (一)构建其层次结构模型如图1 所示。
 目标层 目标层
 准则层 准则层
 方案层 方案层
(二)建立判断矩阵,并用特征值法求出权重
(1)建立判断矩阵A-B(相对于产品方案选择,成本、功能和外观准则间的相对重要性比较)
   A-BA B1 B2B3Wi A-BA B1 B2B3Wi
B1 13 50.6370 CI=0.0193
B21/31 30.2583 CR=0.0332<0.1
B31/5 1/3 10.1047
(2)建立判断矩阵B1- C(相对于产品成本准则,各产品方案之间相对重要性比较)
   B1-C B1 C1 C2 C3 C4Wi B1-C B1 C1 C2 C3 C4Wi
C1 17 3 40.5737 CI=0.0355
C21/7 1 1/21/3 0.0744CR=0.0394<0.1
C31/3 2 12 0.2036
C41/43 1/2 10.1483
(3)建立判断矩阵B2- C(相对于产品功能准则,各产品方案之间相对重要性比较)
   B2-C B2 C1 C2 C3Wi B2-C B2 C1 C2 C3Wi
C1 15 2 0.5816CI=0.0019
C21/5 11/3 0.1095CR=0.0033<0.1
C31/2 3 10.3089
(4)建立判断矩阵B3- C(相对于产品外观准则,各产品方案之间相对重要性比较)
   B3-C B3 C2 C3 C4 Wi B3-C B3 C2 C3 C4 Wi
C2 11/6 1/5 0.5816CI=0.0429
C36 11/2 0.1095CR=0.0739<0.1
C45 2 10.3089
(三)求出各备选方案对总目标的优先等级
由A-B判断矩阵求出三个子目标对总目标的权系数,其他三个矩阵是求各措施方案对各子目标的优先等级企业管理论文,或实现各子目标的重要程度,有了各方案对各子目标的权重,又有了各子目标对总目标的权重,就可以通过加权的办法求出各备选方案对总目标的优先等级。
 = =
式中: ——第i项措施对总目标的权重; ——第i项措施对总目标的权重; ——第i个子目标对总目标的权重; ——第i个子目标对总目标的权重; ——第j项措施对第i项子目标的权重;用矩阵表示如下: ——第j项措施对第i项子目标的权重;用矩阵表示如下:
 = = 
 由此,在前面的基础上进行层次总排序,其结果如下表所示: 由此,在前面的基础上进行层次总排序,其结果如下表所示:
层 B1B2 B3 方案层总 方案
次 0.6370 0.2583 0.1047 排序权重 排序
 C1 0.5737 0.5816 0.0000 0.51571 C1 0.5737 0.5816 0.0000 0.51571
C2 0.0744 0.1095 0.5816 0.08434
C3 0.2036 0.3089 0.1095 0.24802
C4 0.1483 0.0000 0.3089 0.15203
四、结论
通过以上计算结果可以知道,对于企业选择产品方案,所考虑的四种备选方案的相对总排序权重为:方案C1为0.5157;方案C2为0.0843;方案C3为0.2480;方案C4为0.1520。因此,企业应选择方案C1作为产品方案的设计。层次分析法可以用于企业产品方案的选择问题,同时它还可以较好地解决目标的矛盾性、决策人的偏好等因素带来的决策难点。另外,在应用层次分析法时应注意判断矩阵的维度不要太高,维度≤6为最佳;可以对同一问题建立若干个层次结构,然后将其产生的不同结果反馈给决策者,征询他们对不同层次结构分析结果的满意度,进行取舍;还可以采用群体决策,并用判断矩阵评分算术平均法、判断矩阵评分几何平均法、权重算术平均法来进行综合判断。
参考文献:
[1].彭勇行.管理决策分析[M].科学出版社,2000,10
[2].钱颂迪.运筹学[M].清华大学出版社,1990.
[3].吴君民,宁宣熙.层次分析法在企业财务决策中的应用探讨[J].财会通讯,2005(04):32-34
[4].黄灏然,俞守华.层次分析法在价值工程中的应用[J].价值工程,2006(10):59-61
|


