| 从表1可以看出，上证和深证综指收益率均值大于0，偏度小于0，表明我国股市近15年来上涨的天数大于下跌的天数，每天上涨的平均幅度也高于每天下跌的平均幅度。两序列的峰度都大于3，JB统计量也至少在99%的置信水平上拒绝了序列为正态分布的假设。从而我们可以得知，沪深两市综指收益率序列具有“尖峰厚尾”特征。
3.2Copula模型参数的估计结果与评价
当样本数量很大时，核函数的选取对估计结果影响不大，因此本文选用光滑性良好的正态核函数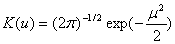 。核函数选定后，窗宽是影响估计结果一个重要因素。通过前文分析，上证和深证综指收益率序列具有尖峰、厚尾特性，依据Bowman(1997)提出窗宽选择原理得到上证和深证综指非参数核密度估计的光滑参数分别为 ；由此得到两市综指收益率核密度估计为 ，如图1所示：基本拟合了沪深股市综指收益率分布的“尖峰厚尾”特征。
图3.1沪深两市核密度估计图
依据Copula函数的特性，对沪深综指收益率核密度函数概率积分变换计算 的估计值 。从图3.2我们可以看出，序列大致服从标准的均匀分布；通过ks统计检验，在5%置信度下，p-value值分别为0.3583、0.3900，从而进一步证明了序列确实来自标准均匀分布。
图3.2u、v经验分布与标准均匀分布CDF
为了考察M-copula函数对金融市场之间的相关程度刻画能力，本文另外选取Gumbel、Clayton、FrankCopula函数来描述沪深综指收益率序列间的相关结构，得到如表3.2所示的参数估计结果。
表3.2中Copula函数能否拟合沪深股市收益率序列的相关结构，本文给出了Copula函数与标准均匀分布的对比图（Q-Q图），如图3.3。从图3.3中我们可以看出，Frankcopula离均匀分布距离较远，拟合样本能力最差；其它拟合ArchimendeanCopula离均匀分布距离不远，散点图相似，基本拟合我国沪深股票市场的相关结构。进一步考察Gumbel、ClaytonCopula和M-Copula函数描述我国沪深股市相关结构的能力，本文利用K-S检验了三种Copula是否服从均匀分布，如表2(K-S拟合分布检验)所示：Gumbel、ClaytonCopula和M-Copula函数对沪深股市综指收益率序列的相关程度刻画能力存在很大差别。根据K-S拟合分布检验的距离，M-Copula对样本的拟合能力最强。从估计得到M-Copula函数的权重系数，沪深股市综指收益率序列的尾部，两市之间的相关性都增强且存在非对称的尾部相关结构。
表3.2Copula函数的参数估计结果
|
名称
|
参数
|
SH-SZ
|
似然对数值
|
K-S拟合分布检验
|
|
距离
|
P-value
|
|
Frank
|
|
12.139
|
2362.426
|
0.2427
|
2.20E-16
|
|
Gumbel
|
|
3.248
|
2394.857
|
0.1446
|
2.20E-16
|
|
Clayton
|
|
3.534
|
2208.033
|
0.1193
|
2.20E-16
|
|
M-copula
|
|
11.322
|
2021.095
|
0.1103
|
2.20E-16
|
|
|
3.418
|
|
|
3.671
|
|
|
0.0156
|
|
|
0.4712
|
|
|
0.5132
|
Gumbel和ClaytonCopula函数能够非对称性捕捉到股票市场上、下尾部的相关结构，然而在复杂多变的金融市场中，它们往往也低估股票市场下、上尾部的相关程度。本文选取的样本数据时间跨度很大，股票市场经过多次的牛、熊市交替，单一Copula函数不能最优描述股票市场的相关结构，K-S拟合分布检验的距离也印证了M-Copula模型较为准确刻画了金融市场之间的相关程度，捕捉了我国股票市场从1996年至今熊、牛市交替的相关模式。
4结语
金融风险管理中，经常遇到金融资产尾部相关性分析问题，Copula函数为分析这类问题提供了有力的工具。然而，由于金融市场之间相关关系非常复杂，实际应用中很难用单一的Copula函数描述金融市场之间的各种相关模式，尤其
图3.3ArchimedeanCopula的散点图
熊、牛股市交替的金融市场。本文通过线性组合ArchrimedeanCopula构建非参数核密度估计M-copula函数，并对沪深股市的相关性进行了实证分析，结果显示：与Clayton、Gumbel和FrankCopula函数相比，M-Copula函数能够全面准确捕捉到我国沪深股票市场相关关系的变化。相对于单一ArchimedeanCopula函数，M-Copula是一种更为灵活、实用性更强的金融分析工具，不过更多的ArchimedeanCopula函数和金融资产组合模型还须进一步研究。
参考文献
1 Bowman A W, Azzalini A.AppliedSmoothing Techniques for Data Analysis[M].Oxford UniversityPress,1997.
2 Durrleman V,Nikeghbai A.Finaancial Econometrics Research Centre[M].London:City University,2000.
3 Nelsen R B. An Introduction to Copulas[M].Springer Verlag,New York,1998.
4 De Metteis R.Fitting Copulas to data[D].Diphoma Thesis,Institute of Mathematics of theUniversity of Zurich,2001:38-39.
5 赵丽琴.Copula函数的非参数核密度估计[J].统计与决策,2009(9):28-31.
6 孙志斌.Copula理论在金融分析中的应用[J].广西师大学报,2004,22(2):47-52.
7 韦艳华、张世英.Copula理论及其在金融分析上的应用[M].北京:清华大学出版社,2008. 2/2 首页 上一页 1 2 |
