三、由表5-1中的 的值和(4)、(5)可以求得 的值和(4)、(5)可以求得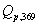 、再由(7)计算 、再由(7)计算 ,最后由(8)计算 ,最后由(8)计算 得: 得:

四、把 、 、 、 、 和 和 (取表5-4的值)代入(11)中得到: (取表5-4的值)代入(11)中得到:
 。 。
五、根据上述得出的投资组合里资产的权重 对第一步中选取的资产周收益率进行组合,得到优化后投资组合的周收益率序列。图1为三者的比较。 对第一步中选取的资产周收益率进行组合,得到优化后投资组合的周收益率序列。图1为三者的比较。
|
资产及其组合
|

|

|

|
|
招商银行
|
-0.27%
|
0.05482
|
-0.04925
|
|
中国石化
|
-0.3%
|
0.05362
|
0.055949
|
|
格力电器
|
1.65%
|
0.04177
|
0.39502
|
|
悦达投资
|
2.9%
|
0.07819
|
0.370891
|
|
海通证券
|
0.39%
|
0.07300
|
0.053425
|
|
辽宁成大
|
0.47%
|
0.08252
|
0.056956
|
|
原比例组合
|
0.83%
|
0.04453
|
0.186366
|
|
最优组合(常相关系数)
|
2%
|
0.076329
|
0.262023
|
|
2.5%
|
0.077363
|
0.323153
|
表2

图1
3.3实证结果分析
(1)从表2我们可以看出,保险公司的资产组合与各个资产的方差相比,比任何单个资产的方差都小,但经过动态风险控制模型下的最优资产组合的方差更小,并且从表2中可以看出,优化投资组合具有的标准差和最大的夏普比,并且收益率也较原来的资产组合大许多。这表明动态风险控制模型确实控制了风险和减少了风险的传染性,降低了投资组合的风险水平。
(2)该模型不仅考虑了收益率的风险,同时还固定了收益率,选取的周收益率为2%,该值已远高于原投资组合的收益率,说明该模型具有现实意义。
(3)本文选取了GARCH模型来描述单项资产的收益率波动性比较符合当前的股票市场波动。
(4)另外,本文的实证只是考虑了前19期对第20期收益率得影响,当然,我们也可以研究前30期或更多的对后一期的影响
参考文献:
[1]M arkow itz H.Portfolio selection [J]. Journal of Finance, 1952, 7: 77~ 91.
[2]OuderriB N ,Sullivan W G. A semi-variance model for incorporating risk into capitalinvestment analysis[J]. Journal of Engineering Economist, 1991, 2: 211~ 223.
[3]Green R C,Hollifield B. When will mean-varianceefficient portfolio be well diversified?[J]. Journal of Finance, 1992, 47: 1785~1809.
[4]Konno H, Shirakaw a H. Equilibrium relations in a capital asset market, a mean absolutedeviation approach [J ]. F inancial Engineering and the Japanese Markets, 1994,1: 21~ 35.
[5]Konno H, Suzuki T, Kobayash i D. A branch and bound algorithm for solving mean-risk-skewness model[ J ]. Optimization Methods and Software,1998, 10: 297~ 317.
[6]Philippe J. Value at Risk: the new benchmark for controlling market risk [M ]. Chicago: Irw in Professional Publish ing, 1996.
[7]Bollerslev T,Engle R F, Wooldridge J. A capitalasset pricing model with time varyingcovariances [J ]. Journal of Political Economy, 1988, 96: 116~131.
[8]Bollerslev T,Engle R F. Common persistence in conditional variances[J]. Economitrica, 1993,61 (1) :167~ 186
3/3 首页 上一页 1 2 3 |


