| 上述模型中,第一个方程为均值方程,第二个为波动方程,对第二个方程展开如下:
 (3) (3)
其中 是波动方程中的残差滞后项和滞后项的个数, 是波动方程中的残差滞后项和滞后项的个数, 表示选定的参考点。并且上述方程展开可以得到: 表示选定的参考点。并且上述方程展开可以得到:
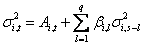 (4) (4)
在 和 和 给定的情况下, 给定的情况下, 是 是 的线性函数。 的线性函数。
2.3资产间常相关系数的确定
如果选择较短的投资时期的话,资产间相关系数的变化比较小,可以用资产间的总体相关系数来作为研究的相关系数,即是一个常数,计算公式如下:

其中: 分别代表资产的收益率序列, 分别代表资产的收益率序列, 为资产收益率的标准差,描述资产 为资产收益率的标准差,描述资产 的GARCH模型的均值方程为 的GARCH模型的均值方程为 ,所以 ,所以 是协方差 是协方差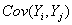 的一致无偏估计量, 的一致无偏估计量, 是 是 的一致无偏估计量,然后根据 的一致无偏估计量,然后根据 ,可得: ,可得:
 (5) (5)
2.4组合衰减方差构建
Markowitz(1952)认为投资组合在第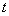 时期的收益率方差-协方差矩阵为: 时期的收益率方差-协方差矩阵为:
 (6) (6)
把(4-24)代入到(4-26)得投资组合方差-协方差矩阵:
 (7) (7)
如果令:
 (8) (8)
 (9) (9)
那么 就是“组合衰减方差”。 就是“组合衰减方差”。 具有以下的经济意义:对于一定的投资组合, 具有以下的经济意义:对于一定的投资组合, 表示投资组合前 表示投资组合前 期收益率方差在影响第 期收益率方差在影响第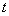 期收益率之前衰减的部分, 期收益率之前衰减的部分, 是投资组合里各个资产权重向量W的函数,当投资组合中各项资产的前 是投资组合里各个资产权重向量W的函数,当投资组合中各项资产的前 期收益率方差给定时GARCH, 期收益率方差给定时GARCH, 的值越大,说明投资组合前 的值越大,说明投资组合前 期收益率方差对 期收益率方差对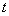 期收益率方差 期收益率方差 的影响越小。通过协同思想,当 的影响越小。通过协同思想,当 时, 时, 成立。从而就可以减少风险传递,因此建立了基于协同持续的动态风险控制模型: 成立。从而就可以减少风险传递,因此建立了基于协同持续的动态风险控制模型:
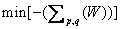

其中: 为每项资产的平均收益率, 为每项资产的平均收益率, 为元素均为1的 为元素均为1的 维向量。用拉格朗尔函数 维向量。用拉格朗尔函数 : :
 满足: 满足:
 (10) (10)
并求解得到:
 (11) (11)
需要说明的是,由于保险公司在资金运用中不允许卖空行为出现,所以,我们在用计算 时,需要加入 时,需要加入 这个约束条件。 这个约束条件。
3 基于平安保险公司的实证研究
3.1研究样本的选择
出于对资料的可获得性,本文主要选取了中国平安2009年年报中证券投资情况里的前10个证券品种来作为研究对象。考虑到这10个证券产品主要是股票,而股票的市场波动性较大,为保证结果的客观性和准确性,选取了较大的样本容量。数据选择为2002年4月12日到2009年12月25日为样本期间,样本期为为388个交易周。由于考虑股票上市时间较晚,数据缺失比较大。最后选择了招商银行、中国石化、格力电器、悦达投资、海通证券和辽宁成大六只股票来作为研究对象。数据来源于清华金融研究数据库。本文实证结果综合利用SPSS统计软件、Eviews经济统计软件、Matrix矩阵软件及EXCEL计算得出。
3.2实证分析
本文的实证数据选择2002年4月12日到2009年12月25日为期间招商银行、中国石化、格力电器、悦达投资、海通证券和辽宁成大六只股票每周收盘价,取对数收益:

实证的步骤如下:
一、利用Eviews软件对单个资产的周集几何收益率 根据AIC准则进行GARCH(p,q)参数估计和资产间相关系数 根据AIC准则进行GARCH(p,q)参数估计和资产间相关系数 的估计,其中 的估计,其中 论文格式。另外,对收益率 论文格式。另外,对收益率 进行GARCH(1,1)的模型参数估计的结果如下表: 进行GARCH(1,1)的模型参数估计的结果如下表:
6只股票的GARCH(1,1)模型参数估计结果
|
股票
|

|

|

|

|
|
招商银行
|
0.012504
|
0.000705
|
0.080594
|
0.740632
|
|
中国石化
|
0.012394
|
0.0000405
|
0.032595
|
0.958098
|
|
格力电器
|
0.018186
|
0.00000917
|
0.038190
|
0.969646
|
|
悦达投资
|
0.010887
|
0.000059
|
0.036403
|
0.967645
|
|
海通证券
|
0.043046
|
0.002844
|
0.254113
|
0.571941
|
|
辽宁成大
|
0.012985
|
0.000019
|
0.269685
|
0.821671
|
表1
二、在单项资产的388个周收益率中,选取最后20周的数据,并统计出各个资产的平均收益率 ,然后从单项资产的收益率数据 ,然后从单项资产的收益率数据 中选取最后19周,统计出各个资产的标准差 中选取最后19周,统计出各个资产的标准差 ( ( )。由前面的迭代方程(3)可以看出,在求 )。由前面的迭代方程(3)可以看出,在求 数值时受初始值 数值时受初始值 的影响,为了更好的对保险公司的投资风险起到控制的作用,本文选取数据中最后20周的第一周作为起始方差 的影响,为了更好的对保险公司的投资风险起到控制的作用,本文选取数据中最后20周的第一周作为起始方差 。另外,考虑到保险公司在一段时间会调整一次资产组合,所以投资时间跨度不宜过长GARCH,所以以20周作为投资时间跨度。 。另外,考虑到保险公司在一段时间会调整一次资产组合,所以投资时间跨度不宜过长GARCH,所以以20周作为投资时间跨度。
2/3 首页 上一页 1 2 3 下一页 尾页 |


