| t= (34.59354) (1.637488) (4.609165) (-4.573294)
 =0.998618 F=6504.874 DW=1.257078 =0.998618 F=6504.874 DW=1.257078
对上述回归及检验结果分析可知,除财政支农支出对人均消费支出的影响显著性稍差以外,其他变量都对人均消费支出有显著的影响。 、F检验也呈现高显著性,整体拟合程度很好,且DW值接近2,不存在明显的自相关问题。 、F检验也呈现高显著性,整体拟合程度很好,且DW值接近2,不存在明显的自相关问题。
协整分析:通过上面的分析可知,上述4个变量都是一阶差分之后是平稳的,四个变量有可能存在协整关系。对残差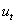 进行单位根检验经济学论文,得到: 进行单位根检验经济学论文,得到:
表2 残差序列单位根检验结果表
|
变量
|
检验类型
|
ADF检验值
|
5%临界值
|
结论
|
|
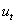
|
(C,T,2)
|
-4.574770
|
-3.574244
|
平稳
|
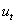 的ADF检验值小于临界值,残差是平稳的。可见,上述4组序列变量存在着长期均衡稳定的关系。 的ADF检验值小于临界值,残差是平稳的。可见,上述4组序列变量存在着长期均衡稳定的关系。
以上进行协整的检验只为得出回归方程,上述的协整检验有一定的局限性,详细的协整检验和得出协整方程将在VAR模型中完成。
六、基于VAR模型的实证分析
(一)VAR模型的引入
VAR模型,即把系统中每一个内生变量作为系统中所有内生变量的滞后值函数来构造的模型。下面矩阵表达式为滞后期1期时的模型表达式,产生了所有包括被解释变量和解释变量的模型表达式。
 = = + +  + +
 =0.996388,F=1724.231。上述模型的表达式是显著的。 =0.996388,F=1724.231。上述模型的表达式是显著的。
(二)Johansen协整检验
通过上面的回归分析可知,上述4个变量一阶差分之后是平稳的,并且是协整的。上述的协整回归有一定的弊端和局限性,我们可以利用Johansen协整检验来得出协整方程表达式。Johansen检验是一种基于向量自回归模型的检验方法,在进行协整检验之前,需要对建立的VAR系统确立合理的滞后期。
要进行Johansen协整检验,需要先根据AIC信息准则和SC信息准则确定其最优滞后期。通过分析比较可知,最优滞后期为3。
Johansen检验表明,在5%的显著性水平下,变量lnct和lnyt、lngt、lnpt之间存在四个协整方程,即四者之间存在长期的稳定均衡关系。具体情况见下表。
表3 Johansen协整检验结果表
|
|
|
|
|
|
|
|
|
|
|
特征值
|
迹统计量
|
临界值
|
P值
|
|
|
|
|
|
|
|
|
|
|
|
0.867041
|
121.8171
|
47.85613
|
0.0000
|
|
0.829673
|
67.33883
|
29.79707
|
0.0000
|
|
0.438749
|
19.54781
|
15.49471
|
0.0116
|
|
0.136194
|
3.952978
|
3.841466
|
0.0468
|
|
|
|
|
|
|
|
|
|
|
Trace testindicates 4 cointegrating eqn(s) at the 0.05 level
被标准化后的协整向量,可以得出的一个不含趋势项、含截距项,包含所有变量的协整方程为:
lnct=0.85lnyt+0.08lngt+1.13lnpt-5.48
分析结果表明:在1978--2008年间,农民人均纯收入、财政支农支出、农村居民消费价格指数与农村居民人均消费之间存在长期动态均衡关系。这表明从长期来看,3个因素对居民人均消费水平的拉动作用是比较显著的。
(1)农民人均纯收入对人均消费的弹性为0.85,即农民人均纯收入每增长1%,农民人均消费增长0.85%;同理,财政支出、农村消费价格指数每增长1%,农民人均消费会增长0.08%和1.13%。
(2)由以上分析结果可知,消费价格指数对农民人均消费影响程度最大,其次是人均纯收入,财政支农支出对农民人均消费影响较小。
(三)VEC模型的设定和估计
如果VAR模型中某些变量之间是协整的,则需要建立一个向量误差修正(VEC)模型,对非约束的VAR模型施加协整约束。VEC模型又被称作向量自回归误差修正模型。误差修正模型是把变量时间序列水平值和差分值建模的优点接合起来,在误差修正模型中同时考虑了短期和长期的调整作用,把变量之间的短期效应和长期关系有效地综合在一起。
以上协整检验说明,Lnct、Lnyt、Lngt和Lnpt四者之间存在协整关系,因此可以建立一个包含协整方程的向量误差修正模型(VEC),这里用Lnct作为被解释变量,Lnyt、Lngt 和Lnpt及其滞后期作为解释变量,可以得到以下误差修正项和误差修正模型:
 = ln = ln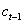 -0.832026ln -0.832026ln -0.108231ln -0.108231ln -1.447281ln -1.447281ln +7.163489 +7.163489
Dlnct=-0.184131*(ln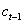 -0.832026ln -0.832026ln -0.108231ln -0.108231ln -1.447281ln -1.447281ln +7.163489) +0.059493Dln +7.163489) +0.059493Dln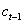 +0.436435Dln +0.436435Dln -0.074957Dln -0.074957Dln +0.365980Dln +0.365980Dln +0.064019 +0.064019
对上面的VEC模型进行分析得到,影响被解释变量的差分项的变动可以分为两部分:
一是自变量的差分对因变量的差分的直接影响。其中,农民人均可支配收入对人均消费量的短期影响弹性为0.436,人均可支配收入对人均消费存在着正向的影响。财政支出对人均消费的短期影响弹性为-0.075,短期内,由于滞后期较短,财政支出也可能对人均消费产生挤出效应。农村消费品价格指数的短期影响弹性为0.366,农村消费品价格指数对人均消费存在着正向的影响。
二是长期均衡关系的调整。方程误差修正系数为-0.184131,在5%的水平下显著。说明长期均衡趋势偏离的收敛机制在起作用。当短期波动偏离长期均衡时,经济系统以-0.184131的调整力度将非均衡状态拉回到均衡状态,协整关系或长期稳定关系对当期的Lnct产生刺激作用。
(四)格兰杰因果检验
协整检验结果告诉我们,山东省的农村人均纯收入、财政支农支出、农村消费价格指数与农村人均消费量之间存在长期的均衡关系,但是这种均衡关系是否构成因果关系,前面的回归并不能够回答这个问题,所以还需要进一步的验证,需要进行格兰杰因果关系检验。
VAR模型下的格兰杰因果检验主要是用来检验一个内生变量是否可以作为外生变量来对待。实质上是检验一个变量的滞后变量是否可以引入到其他变量方程中,一个变量如果受到其他变量的滞后影响,则称他们具有格兰杰因果关系。
格兰杰因果检验显示:当滞后期设定为1时,农村人均纯收入、财政支农支出、农村居民消费价格水平对农村居民人均消费存在因果关系。
表4格兰杰因果检验表
|
|
|
|
|
|
|
|
|
|
|
Null Hypothesis:
|
Obs
|
F-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
LNYT does not Granger Cause LNCT
|
30
|
2.36192
|
0.0654
|
|
LNCT does not Granger Cause LNYT
|
1.45275
|
0.2385
|
|
|
|
|
|
|
|
|
|
|
|
LNGT does not Granger Cause LNCT
|
30
|
5.82765
|
0.0228
|
|
LNCT does not Granger Cause LNGT
|
4.88479
|
0.0358
|
|
|
|
|
|
|
|
|
|
|
|
LNPT does not Granger Cause LNCT
|
30
|
2.75841
|
0.0459
|
|
LNCT does not Granger Cause LNPT
|
0.47399
|
0.4970
|
|
|
|
|
|
|
|
|
|
|
(五)脉冲响应分析
脉冲响应函数反映了来自随机扰动项的一个标准差冲击对内生变量当前和未来取值的影响。在向量自回归模型的基础上,运用脉冲响应函数来考察1978--2008年间农村人均纯收入、财政支农支出、农村居民消费价格水平通过怎样的路径对农村居民人均消费产生影响。
下面4张图是基于VAR的脉冲响应函数曲线,横轴代表响应函数的追踪期,纵轴代表因变量对解释变量的响应程度。图中的实线为响应函数的计算值。
图3 农村人均消费支出对自身的冲击图4 人均纯收入对消费支出的冲击
图5 财政支农支出对人均消费的冲击图6 消费价格指数对人均消费的冲击
图3反映的是人均消费水平对自身的变化的脉冲响应函数图,当给人均消费水平一个正冲击后,引起自身缓慢上升,但增长幅度逐渐趋缓。即人均消费水平的正向冲击对自身的增长具有显著的促进作用,并且这一显著的促进作用具有较长的持续效应。
图4反映的是人均收入水平对人均消费水平变化的脉冲响应函数图,当给人均收入水平一个正冲击后引起人均消费水平增长,但随着滞后期的增加,可能出现不断下降的趋势。这说明有可能存在其他因素的影响。
图5反应的是财政支农支出对人均消费水平的脉冲响应函数图经济学论文,给财政支农支出一个正冲向后,引起其快速上升,并随着滞后期的增加,这种趋势在不断减缓,但具有持续效应。
图6反映的是农村消费价格指数对人均消费水平的脉冲响应函数图,当给农村消费价格指数一个正冲击后,会引起其快速上升,但随着时间的推移,农村消费价格的攀升也会带动农村消费水平的上升。
(六)方差分解
脉冲响应函数是反映系统对一个内在变量的冲击效应,而方差分解是将系统的均方误差分解成各变量冲击所做的贡献。
下面图7反映了山东省人均消费水平、人均收入水平、财政支农支出、农村居民消费价格指数分别对人均消费水平的贡献度。

2/3 首页 上一页 1 2 3 下一页 尾页 |


