论文摘要：新建城市污水厂处理工艺的选择是一个多因素群决策的问题。层次分析法（AHP）是将定量分析与定性分析相结合的综合决策方法，其能为解决这类问题提供依据。AHP法作为新建污水厂处理工艺选择的计算模型兼顾考虑并量化了候选处理工艺的经济、技术和环境性能。AHP法的核心内容是构建新建城市污水厂处理工艺评选的指标体系。指标体系包括具体指标和指标的权重。
论文关键词：城市污水处理厂,层次分析法,指标体系,权重
概述
随着国家对城市水污染防治要求的提高，对城市污水处理率及处理程度的要求越来越高，一些污水处理率不高的城市逐步新建城市污水处理厂。我国现运用于实际生产的城市污水处理工艺众多，有A/O工艺、氧化沟工艺、CASS工艺、CAST工艺、BAF工艺、UNITANK工艺等。每种工艺有其自身的优缺点与使用范围，不同的工艺之间也存在许多共性，如某地新建污水处理厂时，选用的技术可以为A/O工艺、氧化沟工艺或CASS工艺，但具体选用何种工艺最好，不仅需要多名专家考虑各备选工艺特点，还需要考虑新建污水厂实际情况，如气候、地理等自然条件，因此，新建城市污水处理厂处理工艺的选择是一个多属性群决策问题，需要运用一套方法学对其进行评价，从而确定选用处理工艺。层次分析法（AHP）为决策者解决这类问题提供了依据。运用AHP法首先要建立新建污水厂处理工艺评选的指标体系，指标体系包括具体的指标和指标的权重。建立的指标体系包含了城市污水处理工艺经济、技术和环境三方面的主要性能，因此，AHP法作为新建污水厂处理工艺选择的计算模型兼顾考虑并量化了候选处理工艺的经济、技术和环境性能，计算结果有科学依据并易于被决策者接受。
1.AHP法简介
层次分析法（AHP）法是由美国著名运筹学家、匹兹堡大学教授T.L.Saaty提出的。AHP法是将定量分析与定性分析相结合的多目标综合决策方法，将决策者的经验与主观判断用数学方法进行处理。AHP法的核心内容是将评价问题层次化，然后由高到低逐层进行分析判断，最后得出评价结果。AHP法具有众多优点：简单易懂、将思维问题层次化、定量与定性计算相结合、便于决策者与决策执行者沟通等。目前AHP法及其变形方法以在众多领域得到普及运用，如：城市规划、招标评价、教学评价等。
AHP法分析过程分为四步：（1）根据评价对象与评价目标，将问题层次化；（2）选定合适的比例标度，构造判断矩阵；（3）进行层次单排序及一致性检验；（4）进行层次总排序及一致性检验。具体求解过程如图1所示：
图1层次分析法分析过程
将问题层次化是指将问题层层剖析，选择适合各个层次的因素，并按照一定原则将相邻的上下两层因素进行关联，下一层因素是对上一层关联因素的细化和具体化。构造判断矩阵是指专家根据选定的标度对同层次与上一层次某因素相关联的因素两两之间进行比较并赋值而得到的矩阵。本研究采用1-9标度，如表1所示。构造的判断矩阵结构如表2所示。层次单排序是指计算某层次与上一层次某因素相关联的因素之间的权重系数，为了保证单排序的准确性，需要进行单排序一致性检验。层次总排序是指各层因素相对于总目标的权重系数，为了确保总排序是否合理，需要对总排序一致性进行检验。
表11-9标度法判断矩阵标度含义表
|
重要性标度
|
含义
|
|
1
|
表示两个元素相比，具有同等重要性
|
|
3
|
表示两个元素相比，前者比后者比较重要
|
|
5
|
表示两个元素相比，前者比后者明显重要
|
|
7
|
表示两个元素相比，前者比后者非常重要
|
|
9
|
表示两个元素相比，前者比后者极为重要
|
|
2，4，6，8
|
表示上述判断的中间值
|
|
1-9倒数
|
若元素i与元素j的重要性之比为δ ,则元素j与元素i的重要性之比为δ =1/δ
|
| |
|
|
表2构造的判断矩阵结构
|
A
|
B
|
B
|
…
|
B
|
|
B
|
δ
|
δ
|
|
δ
|
|
B
|
δ
|
δ
|
|
δ
|
|
…
|
…
|
…
|
…
|
…
|
|
B
|
δ
|
δ
|
|
δ
|
δ（i,j=1,2…,n）表示因素B与B相对A的重要性标度值。在判断矩阵中,其元素δ满足关系：δ>0(i,j=1,2,…,n)；δ=1（i=1,2,…,n）；δ=1/δ。
2.判断矩阵计算方法
运用专家构造的判断矩阵计算专家对指标权重赋值采用乘积方根法，引入随机一致性比率，对构造的判断矩阵层次单排序和层次总排序一致性进行检验。
（1）层次单排序计算过程：
乘积方根法求解步骤如下：
①构造如表2判断矩阵A；
②计算判断矩阵每一行元素的几何平均值，得矩阵B：
 ;
 （i=1,2,……,n）;
③将矩阵B归一化处理，得到矩阵A最大特征值所对应的特征向量W：
 ；
 ；
（2）层次单排序一致性检验计算过程：
①利用以上求解的W计算判断矩阵最大特征值 ：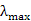
由 得：
 ；
 0；
②计算矩阵的一致性指标C.I.：
 ；
③根据判断矩阵阶数n，查找平均随机一致性指标值R.I.，R.I.值如表3所示：
表3平均随机一致性指标R.I.值
|
阶数n
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
R.I.
|
0
|
0.5149
|
0.8931
|
1.1185
|
1.2494
|
1.3450
|
1.4200
|
|
阶数n
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
R.I.
|
1.4616
|
1.4874
|
1.5156
|
1.5405
|
1.5583
|
1.5779
|
1.5894
|
④计算随机一致性比率C.R.：
 ；
当C.R.时，则认为判断矩阵符合满意一致性要求；否则，认为判断矩阵不符合一致性要求，由此计算的结果误差大，需要重新构造判断矩阵。
（3）层次总排序及一致性检验计算过程：
①首先定义 层与K-1层因素j有关的因素相对于总目标权重系数矩阵， 。
②假定第K-1层j因素相对于总目标的层次总排序权重系数为 ，如果j=2，则即为j因素对总目标的单排序权重系数。第K层与K-1层因素j有关的因素相对于j因素的权重系数向量为C， 。
③计算 ：
 ；
构造的判断矩阵不仅要满足层次单排序一致性检验，同时要满足层次总排序一致性检验。层次总排序检验步骤是从上到下逐步进行的，计算方法如下：
 0
式中： ——第K层与K-1层因素j有关联的因素的一致性指标；
 ——第K层与K-1层因素j有关联的因素的平均一致性指标；
——第K-1层j因素总排序权重系数；
n——第K-1层因素个数。 1/2 1 2 下一页 尾页 |
