| (2)
这里的矩阵 表示第i根桩和第 j根桩的耦合作用,如 表示第i根桩和第 j根桩的耦合作用,如 , ,  则表示第i根桩的单位桩顶力所引起其自身的桩顶位移。 则表示第i根桩的单位桩顶力所引起其自身的桩顶位移。
由于在本文中,承受轴向振动和面内弯曲振动的桥墩也作为柱和梁来处理,因此,其传递矩阵可由通常的柱体及梁的振动理论来推导[17]。设桥墩的状态向量为
, , (3)
其中是第i个桥墩的轴向位移,横向位移及转角, 为其轴向力,剪力及弯矩。设桥墩的传递矩阵为,则对第i个桥墩有
, (4)
这里和 分别是第i个桥墩的顶部和底部的状态向量交通论文,, 是桥墩传递矩阵的子矩阵。 分别是第i个桥墩的顶部和底部的状态向量交通论文,, 是桥墩传递矩阵的子矩阵。
如上所述,假设一个桥墩由一个桩基础支撑,且桩基础和桥墩间采用刚性联结,因此,对第i根桥墩和第i个桩基础有如下关系
, (5)
利用公式(2), (4) 及 (5), 桥墩顶部的位移向量可表示为
(6a)
这里
(6b)
类似地,桥墩顶部的力向量可表示为
(7)
利用上述方程,得如下桥墩顶部的位移向量和力向量间的关系
(8)
这里即为桥墩的阻抗矩阵。上述关系可进一步写成如下的指标形式
, (9)
其中,是阻抗矩阵 的 的 的子矩阵,表示第 i个桥墩和第j个桥墩间的耦合作用。 的子矩阵,表示第 i个桥墩和第j个桥墩间的耦合作用。
3 周期性高架桥结构的非线性特征值方程及其线性近似
如上所述,对面内振动的周期性高架桥结构,横梁的运动同样也包括轴向振动和面内弯曲振动。如图1所示,由于第 j根梁的右端和(j+1)根梁的左端及第j个桥墩的顶部刚性联结,因此有如下的联结条件
, , (10)
这里是第(j+1)根及第j根梁的左端及右端的位移向量。此外,根据第 j个接头处的平衡条件,可得如下方程
, , (11)
这里,是第(j+1)根及第j根梁的左端及右端的力向量论文提纲怎么写。根据横梁轴向振动及面内弯曲振动的控制方程[17],可类似地推导其传递矩阵,因此有
(12)
其中是横梁的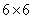 的传递矩阵, 的传递矩阵,  是第j根横梁的左端和右端的状态向量,是单元内横梁长度。利用公式(10)和(11),并令 j号单元为中心单元( 是第j根横梁的左端和右端的状态向量,是单元内横梁长度。利用公式(10)和(11),并令 j号单元为中心单元( ), 则一号单元横梁左端的状态向量可表示为 ), 则一号单元横梁左端的状态向量可表示为
(13)
把由式(9)所确定的表达式代入(13)得
(14)
根据Bloch定理[12], 有 , 这样上述方程可写为 , 这样上述方程可写为
(15a)
其中
, (15b)
上式中为格波波数,此外,上式中的不包括 项。在方程 (12)中令 项。在方程 (12)中令 并代入(15a),并对(15a)左端应用Bloch定理[12],得如下高架桥结构多项式形式的特征值方程 并代入(15a),并对(15a)左端应用Bloch定理[12],得如下高架桥结构多项式形式的特征值方程
(16a)
上式中为多项式特征值方程的系数矩阵,且
, ,
, (16b)
2/3 首页 上一页 1 2 3 下一页 尾页 |


