| 这时,各层对应的弹性材料剪切模量分别为:
 (9) (9)
 (10) (10)
 (11) (11)
其中上标e表示弹性材料。
该裂纹问题的边界条件为:
 (12) (12)
 (13) (13)
 (14) (14)
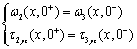 (15) (15)
 (16) (16)
其中式(14)的上标(1)和(2)分别表示FGM界面层内裂纹的上下侧材料。
在反平面剪切状态下,平衡方程为:
 (17) (17)
弹性材料的本构方程为:
 , ,  (18) (18)
将式(18)代入式(17)并作关于坐标x的Fourier变换得:
  (19) (19)
式中,Fourier变换定义为 。 。
将式(9)~(11)代入方程(19)可得其解析解:
 (20) (20)
其中, , , , , 、 、 、 、 和 和  均为关于 均为关于 的未知函数。 的未知函数。
对式(20)作Fourier反变换并应用本构方程(18)得:
  (21) (21)
 (22) (22)
为了得到奇异积分方程,引入位错密度函数:
 (23) (23)
对 有连续性条件: 有连续性条件:
 , , (24) (24)
由式(12)~(16)以及式(21)~(24)可以得到Cauchy奇异积分方程和位移单值条件方程:
 (25) (25)
其中, 为裂纹处材料的初始剪切模量, 为裂纹处材料的初始剪切模量, , , , , , , , , 的具体形式见附录。 的具体形式见附录。
弹性材料的Ⅲ型应力强度因子定义为(以裂纹右尖端为例):
  (26) (26)
函数 在 在 处具有平方奇异性,因此可以将其表示为: 处具有平方奇异性,因此可以将其表示为:
 (27) (27)
将 被 被 标准化处理,并由式(26)可得: 标准化处理,并由式(26)可得:
 (28) (28)
由式(23)和(27)可得,裂纹张开位移为:
 (29) (29)
根据Erdogan提出的配点法可以求得方程组(25)的数值解,进而得到 和 和 。 。
2.2粘弹性解
由FGM的粘弹性对应原理,Ⅲ型应力强度因子和裂纹张开位移的粘弹性解分别为:
 (30) (30)
 (31) (31)
其中, 和 和 分别是 分别是 和 和 的Laplace变换,p是变换参量, 的Laplace变换,p是变换参量, 表示Laplace反变换。 表示Laplace反变换。
3结果与分析
计算时,设定 、 、 以及 以及 ,下文图3~图7中 ,下文图3~图7中 。函数 。函数 和 和 分别取为: 分别取为: 和 和 ,其中 ,其中 和 和 分别是材料(3)的初始和稳态模量, 分别是材料(3)的初始和稳态模量, 和 和 均为时间常数。另外,将应力强度因子和裂纹张开位移分别无量纲化: 均为时间常数。另外,将应力强度因子和裂纹张开位移分别无量纲化: , , 。 。
3.1应力强度因子
由图2可知,对于裂纹靠近FGM界面层中间位置时( )的情形,在不同 )的情形,在不同 条件下,随着l的增大,0时刻的应力强度因子先迅速减小后趋于稳定。当 条件下,随着l的增大,0时刻的应力强度因子先迅速减小后趋于稳定。当 时, 时, 对应力强度因子的影响较明显,其中 对应力强度因子的影响较明显,其中 越大,应力强度因子越小。 越大,应力强度因子越小。
由图3可知,裂纹位置对应力强度因子的影响显著。其中l较小时,裂纹位置越靠近FGM上端,应力强度因子越小,而l较大时应力强度因子的变化趋势则相反。

图2不同均质材料初始模量比时应力强度因子随l的变化
Fig.2Variationsofstressintensityfactorswithlfordifferentinitialrelaxationmodulusratesofhomogeneousmaterials

图3不同裂纹位置时应力强度因子随l的变化
Fig.3Variationsofstressintensityfactorswithlfordifferentcracklocations

图4应力强度因子随时间 的变化 的变化
Fig.4Variationsofstressintensityfactorswith
由图4可以看出,随着时间的推移,不同l影响下应力强度因子始终保持一定的差距,并且按加载函数(指数)形式减小。当 时,三种情况下的应力强度因子均减小到0.6以下。 时,三种情况下的应力强度因子均减小到0.6以下。
由以上各图可知,在不同的 以及裂纹位置影响下,l对应力强度因子的影响规律也不同。由式(7)可知,FGM等效非均匀性参数 以及裂纹位置影响下,l对应力强度因子的影响规律也不同。由式(7)可知,FGM等效非均匀性参数 和 和 成正比,即l是通过影响 成正比,即l是通过影响 进而影响应力强度因子。注意到图3中三条曲线在 进而影响应力强度因子。注意到图3中三条曲线在 处近似交于一点,因为这时 处近似交于一点,因为这时 ,三种情况下裂纹都可看成置于均质无限长的板条之中,仅位置有所不同,此时应力强度因子差别很小。由以上分析可知,在 ,三种情况下裂纹都可看成置于均质无限长的板条之中,仅位置有所不同,此时应力强度因子差别很小。由以上分析可知,在 和裂纹位置一定的情况下,可以通过控制FGM两侧均质材料的松弛模量时间因子比值来减小裂纹的应力强度因子,从而提高材料的抗断裂能力。 和裂纹位置一定的情况下,可以通过控制FGM两侧均质材料的松弛模量时间因子比值来减小裂纹的应力强度因子,从而提高材料的抗断裂能力。 2/3 首页 上一页 1 2 3 下一页 尾页 |


