论文摘要:研究了介于两粘弹性均质材料之间的粘弹性功能梯度界面层模型反平面裂纹问题。通过引入两均质材料松弛模量时间因子比l,给出了功能梯度界面层的一种广义剪切松弛模量,比已有文献中的松弛模量更具有一般性。采用Fourier变换推导出Cauchy奇异积分方程,通过配点数值方法得到应力强度因子和裂纹张开位移的弹性解,并由功能梯度材料的粘弹性对应原理和Laplace变换得到粘弹性解。考察了l值、裂纹位置等参数对应力强度因子和裂纹张开位移的影响。
论文关键词:功能梯度材料,粘弹性,剪切松弛模量,裂纹,对应原理,反平面
0引言
功能梯度材料(FGM)作为一种新型的多相材料,在许多工程领域都有重要的应用,而断裂力学分析则是其中的一个热点问题。为了方便求解,人们往往将FGM的模量假定为某种函数,比如指数或幂函数形式,研究不同裂纹在不同载荷下的应力场。近年来,学者们发展了一类分层模型有效地实现了FGM模量任意变化时的近似解析求解,该模型是将FGM分成若干子层并采用均匀材料或特定函数表示各子层中模量的梯度变化。在FGM界面方面,Li等根据界面两侧材料力学性能函数及各阶导数是否连续对界面进行了分类,并研究了FGM界面间断性对裂纹应力强度因子的影响。
在高温的环境下FGM会体现蠕变和应力松弛的特性,因此,研究FGM的粘弹性断裂问题具有重要的意义。由于粘弹性FGM的松弛模量随空间和时间变化,这给问题求解带来了一定的困难。Herrmann和Schovanec对粘弹性非均匀材料的Ⅲ型裂纹扩展问题进行了研究,其推导过程较为复杂。为了简化求解,Paulino等提出了FGM的粘弹性对应原理,并对粘弹性FGM反平面和平面裂纹问题进行了研究。应用该原理,李伟杰等和Pan等用有限元方法分别研究了粘弹性FGM单一和多重裂纹问题,Cheng等采用分层模型研究了热粘弹性FGM涂层裂纹问题。
FGM的粘弹性对应原理要求其松弛模量为时间-空间分离的形式。应用该对应原理推导裂纹问题的理论解时,一般情况下FGM的松弛模量采用和空间坐标无关的时间因子 ,这对于粘弹性FGM板条比较适用。但对于介于两均质材料之间的FGM界面层模型,当两均质材料松弛模量时间因子不同时,为了保证模型中材料模量在任意时刻连续,FGM松弛模量的时间因子应在空间位置上呈现梯度变化,在可推导出控制方程解析解的前提下,这样的时间因子一般难以确定。这里仅Paulino等给出了一种FGM的与空间坐标相关的时间因子 ,这对于粘弹性FGM板条比较适用。但对于介于两均质材料之间的FGM界面层模型,当两均质材料松弛模量时间因子不同时,为了保证模型中材料模量在任意时刻连续,FGM松弛模量的时间因子应在空间位置上呈现梯度变化,在可推导出控制方程解析解的前提下,这样的时间因子一般难以确定。这里仅Paulino等给出了一种FGM的与空间坐标相关的时间因子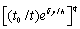 ,并应用在文献[19]和[20]中。遗憾的是,该时间因子只能使两均质材料和FGM界面层的松弛模量在时间上以幂函数形式变化,这样很大程度上限制了FGM的粘弹性对应原理在实际中的应用。为此,本文根据材料的连续性要求,进一步分析该对应原理的适用条件,给出FGM界面层一种广义剪切松弛模量函数。以模型的反平面裂纹问题为例,通过积分变换推导奇异积分方程,并进行数值求解。应用FGM的粘弹性对应原理得到应力强度因子和裂纹张开位移的粘弹性解,并讨论所建模型中多个参数对它们的影响规律。 ,并应用在文献[19]和[20]中。遗憾的是,该时间因子只能使两均质材料和FGM界面层的松弛模量在时间上以幂函数形式变化,这样很大程度上限制了FGM的粘弹性对应原理在实际中的应用。为此,本文根据材料的连续性要求,进一步分析该对应原理的适用条件,给出FGM界面层一种广义剪切松弛模量函数。以模型的反平面裂纹问题为例,通过积分变换推导奇异积分方程,并进行数值求解。应用FGM的粘弹性对应原理得到应力强度因子和裂纹张开位移的粘弹性解,并讨论所建模型中多个参数对它们的影响规律。
1粘弹性FGM界面层模型的广义剪切松弛模量
模型如图1所示,(1)和(3)分别表示上下两均质材料,中间FGM界面层内设置平行于x轴,长度为2a的裂纹,裂纹面处承受纯剪切载荷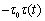 ,其中 ,其中 为时间的无量纲函数。 为时间的无量纲函数。

图1功能梯度界面层裂纹
Fig.1Acrackinthefunctionallygradedinterfacialzone
各层材料的剪切松弛模量可写成初始模量和时间因子相乘的形式:
 (1) (1)
式中上标v代表粘弹性材料,下标1~3分别表示各层序号, 表示空间矢量。 表示空间矢量。
假设各层松弛模量时间因子分别为 、 、 和 和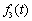 ,根据FGM的粘弹性对应原理适用条件, ,根据FGM的粘弹性对应原理适用条件, 应为空间因子 应为空间因子 和无量纲函数 和无量纲函数 分离的形式: 分离的形式:
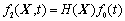 (2) (2)
根据各层材料松弛模量的连续性要求,FGM两侧界面处时间因子应连续变化,由式(2)得:
 (3) (3)
 (4) (4)
由式(3)和(4)得,
  (5) (5)
式中l表示两均质材料松弛模量时间因子比。显然,为了应用FGM的粘弹性对应原理,两时间因子 和 和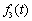 的比值应为常数,即l和时间t无关,这也同时说明了该对应原理的局限性。 的比值应为常数,即l和时间t无关,这也同时说明了该对应原理的局限性。
由式(3)~(5)可知,可以根据l确定合适的 ,进而由式(1)和(2)确定 ,进而由式(1)和(2)确定 ,其中 ,其中 的形式可以任意选择。值得注意的是,FGM界面层对应的弹性材料模量 的形式可以任意选择。值得注意的是,FGM界面层对应的弹性材料模量 应使控制方程有解析解。 应使控制方程有解析解。
本文在计算时,假设 为空间坐标y的指数函数形式 为空间坐标y的指数函数形式 ,并由式(5)构造 ,并由式(5)构造 ,则FGM界面层广义剪切松弛模量为 ,则FGM界面层广义剪切松弛模量为 。已有文献中与空间坐标无关的时间因子 。已有文献中与空间坐标无关的时间因子 可看成 可看成 时的情形,而时间因子 时的情形,而时间因子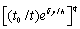 可看成 可看成 , , 时的特例。 时的特例。
将上述函数形式化简,并由式(1)、(3)和(4)可得,各层材料剪切松弛模量分别为:
 (6) (6)
 (7) (7)
 (8) (8)
其中, , ,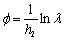 。 。
由式(6)~(8)可知,各层材料的剪切松弛模量可以同时在时间上任意变化,这比已有文献中的松弛模量函数有了很大的扩展。因此,本文给出的广义剪切松弛模量更具有一般性。
2反平面裂纹问题的求解
2.1弹性解
以反平面裂纹问题为例,根据FGM的粘弹性对应原理,首先计算应力强度因子和裂纹张开位移的弹性解。 1/3 1 2 3 下一页 尾页 |


