定义薄体区域特征值最小尺寸与最大尺寸之比 为狭长比。表1列出了不同狭长比下,边界点 为狭长比。表1列出了不同狭长比下,边界点 和内点 和内点 上温度的计算结果。表2和表3分别给出了不同狭长比下, 上温度的计算结果。表2和表3分别给出了不同狭长比下, 点热流和 点热流和 点温度梯度 点温度梯度 的计算结果。表4给出了当狭长比 的计算结果。表4给出了当狭长比 时,直线 时,直线 上内点温度梯度的计算结果。图34描绘了当 上内点温度梯度的计算结果。图34描绘了当 时,边界点 时,边界点 处的热流与内点 处的热流与内点 点温度梯度 点温度梯度 的收敛曲线。 的收敛曲线。
   
表1表明,即使狭长比达到1.0E-10,本文在边界点与内点处的温度数值解与精确解仍十分地吻合。从表2可看出,当狭长比为1.0E-02时,常规边界元法所算得的边界点处的热流已开始失效,随着狭长比的继续减小,计算结果则完全失真。相比较,即使狭长比为1.0E-10,本文在边界点 处的热流数值解与精确解仍十分地接近。表明,本文方法求解狭长比达 处的热流数值解与精确解仍十分地接近。表明,本文方法求解狭长比达 的超薄涂层结构十分地有效。 的超薄涂层结构十分地有效。
从表3可看出,在计算内点温度梯度时,常规边界元法求解狭长比为1.0E-02的结构已失效,而本文算法可准确计算到狭长比为1.0E-10的结构。表4的数据进一步表明,本文方法对内点位置不加限制,即使狭长比为1.0E-09时,不同内点上的温度梯度的计算精度相近而且很高。图34的温度梯度 与热流误差曲线表明,即使狭长比达到1.0E-09,方法仍具有良好的收敛特性。 与热流误差曲线表明,即使狭长比达到1.0E-09,方法仍具有良好的收敛特性。
例2矩形涂层结构的热流问题,涂层的厚度为 ,基体的厚度为 ,基体的厚度为 ,宽度为 ,宽度为 ,涂层与基体的导热率分别为 ,涂层与基体的导热率分别为 , , ,边界条件如图45所示。将边界离散成40个线性单元,边界函数采用二次不连续插值逼近。 ,边界条件如图45所示。将边界离散成40个线性单元,边界函数采用二次不连续插值逼近。
当涂层厚度 从1.0E-01~1.0E-10变化时,表5列出了边界点 从1.0E-01~1.0E-10变化时,表5列出了边界点 处的热流数值解,图56与表6分别给出了内点 处的热流数值解,图56与表6分别给出了内点 处的温度与梯度的计算结果。当涂层厚度 处的温度与梯度的计算结果。当涂层厚度 时,表7给出了直线 时,表7给出了直线 上内点处的梯度数值解,图7给出了内点 上内点处的梯度数值解,图7给出了内点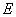 上的梯度 上的梯度 ,边界点 ,边界点 上的热流的收敛曲线。 上的热流的收敛曲线。
从表5可看出,当涂层的厚度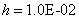 时,常规边界元法在边界点 时,常规边界元法在边界点 处的热流解的精度已经比较差,随着 处的热流解的精度已经比较差,随着 的继续减小,结果则完全失真。相比较,即使 的继续减小,结果则完全失真。相比较,即使 时,本文在边界点 时,本文在边界点 处的热流解与精确解仍十分地吻合。 处的热流解与精确解仍十分地吻合。
 
图56与表6的数据表明,当涂层厚度小到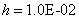 时,常规边界元法的内点 时,常规边界元法的内点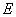 处的温度数值解已经偏离精确解,内点 处的温度数值解已经偏离精确解,内点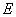 处的梯度数值解已完全失效。对厚度小到 处的梯度数值解已完全失效。对厚度小到 的结构,本文在内点 的结构,本文在内点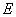 处的温度与梯度数值解与精确解仍十分地接近。 处的温度与梯度数值解与精确解仍十分地接近。
图7的误差曲线表明,当涂层的厚度为 时,本文方法具有良好的收敛特性。 时,本文方法具有良好的收敛特性。
   
img3
0
4结论
本文对涂层结构材料的温度场进行了研究,成功地计算了涂层表面的温度、热流及内点的温度、梯度。在关键的涂层域计算中,采用二次单元逼近几何边界,使得准确计算超薄的涂层结构成为可能;基于规则化边界积分方程计算奇异积分;对求内点物理量及边界量时产生的几乎奇异拟奇异积分,采用一类非线性变量替换法,有效地改善了几乎奇异拟奇异核的特性,使几乎奇异拟奇异积分的计算可以通过普通的高斯求积公式精确地完成。从算例可看出,即使对厚度小到 或者狭长比达 或者狭长比达 的涂层结构,本文方法依然可准确地求解。表明了方法的可行性和有效性。 的涂层结构,本文方法依然可准确地求解。表明了方法的可行性和有效性。
参考文献
1.胡兴军.刀具表面涂层技术进展综述[J].产品与技术,2008,12(6):91-94.(HuXJ.Commentontheprogressofcuttingtoolcoatingtechnology[J].Products&Technology,2008,12(6):91-94.(inChinese))
2.陈克,黄德武.MCA方法在金属材料涂层性能研究中的应用[J].计算力学学报,2003,20(4):473-477.(ChenK,HuangDW.ApplicationofMCAmethodonstudyofcoatingmaterialproperties[J].ChineseJournalofComputationalMechanics,2003,20(4):473-477.(inChinese))
3.程长征,牛忠荣,周焕林,杨志勇.涂层结构中温度场的边界元分析[J].合肥工业大学学报,2006,29(3):326-329.(ChengCZ,NiuZR,ZhouHL,YangZY.Boundaryelementanalysisofthetemperaturefieldinthecoating-structures[J].JournalofHefeiUniversityofTechnology,2006,29(3):326-329.(inChinese))
4.姚振汉,杜庆华.边界元法应用的若干近期研究及国际新进展[J].清华大学学报,2001,41(4):89-93.(YaoZH,DuQH.Somerecentinvestigationsandnewprogressesintheapplicationofboundaryelementmethods[J].JournalofTsinghuaUniversity,2001,41(4):89-93.(inChinese))
5.DuF,LovellMR,WuTW.Boundaryelementmethodanalysisoftemperaturefieldsincoatedcuttingtools[J].InternationalJournalofSolidsandStructures,2001,38:4557-4570.
6.孙焕纯.无奇异边界元法[M].大连:大连理工大学出版社,1999,4.(SunH.C.NonsingularBoundaryElementMethod[M].Dalian:DalianUniversityofTechnologyPress,1999,4(inChinese))
7.CruseTA.Animprovedboundaryintegralequationmethodforthreedimensionalelasticstressanalysis[J].Computers&structures,1974,4:741-754.
8.高效伟,Ch.Zhang.非均质问题中的无网格边界单元法[J].固体力学学报,2006,27:62-69.(GaoXW,ZhangC.MeshlessBEMinnonhomogeneousproblems[J].ActaMechanicaSolidaSinica,2006,27:62-69.(inChinese))
9.JunL,BeerG,MeekJL.EfficientevaluationofintegralsoforderusingGaussquadrature[J].EngineeringAnalysis,1985,2:118-123.
10.GaoXW,YangK,WangJ.Anadaptiveelementsubdivisiontechniqueforevaluationofvarious2Dsingularboundaryintegrals[J].EngineeringAnalysiswithBoundaryElements,2008,32:692–696.
11.GaoXW,DaviesTG.Boundaryelementprogramminginmechanics[M].CamberidgeUniversityPress,2002.
12.LutzEL.ExactGaussianquadraturemethodsfornear-singularintegralsintheboundaryelementmethod[J].EngineeringAnalysiswithBoundaryElements,1992,9:233-245.
13.TellesJCF.Aself-adaptivecoordinatetransformationforefficientnumericalevaluationofgeneralboundaryelementintegral[J].InternationalJournalforNumericalMethodsinEngineering,1987,24:959-973.
14.SladekV,SladekJ,TanakaM.OptimaltransformationsoftheintegrationvariablesincomputationofsingularintegralsinBEM[J].InternationalJournalforNumericalMethodsinEngineering,2000,47:1263-1283.
15.JohnstonPR.Applicationofsigmoidaltransformationstoweaklysingularandnearsingularboundaryelementintegrals[J].InternationalJournalforNumericalMethodsinEngineering,1999,45:1333-1348.
16.MaH,KamiyaN.Distancetransformationforthenumericalevaluationofnearsingularboundaryintegralswithvariouskernelsinboundaryelementmethod[J].EngineeringAnalysiswithBoundaryElements,2002,25:329-339.
17.张耀明,孙翠莲,谷岩.边界积分方程中近奇异积分计算的一种变量替换法[J].力学学报,2008,40(2):207~214.(ZhangYM,SunCL,GuY.Theevaluationofnearlysingularintegralsintheboundaryintegralequationswithvariabletransformation[J].ActaMechanicaSinica,2008,40(2):207-214.(inChinese))
18.牛忠荣,王秀喜,周焕林.边界元法计算近边界点参量的一个通用算法[J].力学学报,2001,33:275~283.(NiuZR,WangXX,ZhouHL.AgeneralalgorithmforcalculatingthequantitiesatinteriorpointsclosetotheboundarybytheBEM[J].ActaMechanicaSinica,2001,33:275-283.(inChinese))
19.周焕林,牛忠荣,王秀喜.二维热弹性力学边界元法中几乎奇异积分的正则化[J].固体力学学报,2004,25(2):144-148.(ZhouHL,NiuZR,WangXX.TheregularizationofnearlysingularintegralsintheBEMoftwo-dimensionalthermoelasticity[J].ActaMechanicaSolidaSinica,2004,25(2):144-148.(inChinese))
20.张耀明,谷岩,陈正宗.位势边界元法中的边界层效应与薄体结构[J].力学学报,2010,42(2):219-227.(ZhangYM,GuY,ChenJT.BoundarylayereffectandthinbodystructureinBEMforpotentialproblems[J].ChineseJournalofTheoreticalandAppliedMechanics,2010,42(2):219-227.(inChinese))
21.PadhiGS,ShenoiRA,MoySSJ,McCarthyMA.AnalyticalIntegrationofkernelshapefunctionproductintegralsintheboundaryelementmethod[J].Computers&structures,2001,79,1325-1333.
22.FratantonioM,RencisJJ.Exactboundaryelementintegrationsfortwo-dimensionalLaplaceequation[J].EngineeringAnalysiswithBoundaryElements,2000,24:325-342.
23.ZhangYM,GuY,ChenJT.BoundarylayereffectinBEMwithhighordergeometryelementsusingtransformation[J].ComputerModelinginEngineering&Sciences,2009,vol.45,no.3,pp.227–247.
24.LuoJF,LiuYJ,BergerEJ.Analysisoftwo-dimensionalthinstructures(frommicro-tonano-scales)usingtheboundaryelementmethod[J].ComputationalMechanics,1998,22:404-412.
25.LuoJF,LiuYJ,BergerEJ.Interfacialstressanalysisformulti-coatingsystemsusinganadvancedboundaryelementmethod[J].ComputationalMechanics,2000,24:448-55.
26.ZhangYM,LuHX,WangLM.NovelRegularizedBoundaryIntegralEquationsforPotentialPlaneProblems[J].AppliedMathematicsandMechanics,2006,27(9):1165-1170.
27.张耀明,温卫东.弹性力学平面问题中一类无奇异边界积分方程[J].力学学报,2004,36(3):311-321.(ZhangYM,WenWD.Akindofnewnonsingularboundaryintegralequationsforelasticplaneproblems[J].ActaMechanicaSinica,2004,36(3):311-321.(inChinese))
参考文献
1 胡兴军. 刀具表面涂层技术进展综述. 产品与技术,2008,12(6):91-94
2 陈克,黄德武. MCA 方法在金属材料涂层性能研究中的应用. 计算力学学报,2003,20(4):473-477
3 程长征,牛忠荣,周焕林,杨志勇. 涂层结构中温度场的边界元分析. 合肥工业大学学报,2006,29(3):326-329
4 姚振汉,杜庆华. 边界元法应用的若干近期研究及国际新进展. 清华大学学报,2001,41(4):89-93
5 Du F, Lovell M R, Wu T W. Boundary element method analysis of temperature fields in coated cutting tools. International Journalof Solids and Structures, 2001, 38: 4557~4570
6 孙焕纯. 无奇异边界元法. 大连:大连理工大学出版社, 1999, 4
7 Cruse T A. An improved boundary integral equation method for three dimensional elastic stress analysis. Compt Struct, 1974, 4:741~754
8 Granados J J, Gallego G. Regularization of nearly hypersingular integrals in the boundary element method. Engng Anal Bound Elem,2001, 25: 165~184
9 Jun L, Beer G, Meek J L. Efficient evaluation of integrals of order using Gauss quadrature. Engng Anal, 1985, 2: 118~123
10 Gao X W, Yang K, Wang J. An adaptive element subdivision technique for evaluation of various 2D singular boundary integrals.Engineering Analysis with Boundary Elements, 2008, 32: 692–696
11 Gao X W, Davies T G. Boundary element programming in mechanics. Camberidge University Press, 2002
12 Lutz E L. Exact Gaussian quadrature methods for near-singular integrals in the boundary element method. Engng Anal Bound Elem,1992, 9: 233~245
13 Telles J C F. A self-adaptive coordinate transformation for efficient numerical evaluation of general boundary elementintegral. Int J Numer Meth Engng, 1987, 24: 959~973
14 Sladek V, Sladek J, Tanaka M. Optimal transformations of the integration variables in computation of singularintegrals in BEM. Int J Numer Meth Engrg, 2000, 47: 1263~1283
15 Johnston P R. Application of sigmoidal transformations to weakly singular and near singular boundary elementintegrals. Int J Numer Meth Engng, 1999, 45: 1333~1348
16 Ma H, Kamiya N. Distance transformation for the numerical evaluation of near singular boundary integrals with various kernelsin boundary element method. Engng Anal Bound Elem, 2002, 25: 329~339
17 牛忠荣,王秀喜,周焕林. 边界元法计算近边界点参量的一个通用算法,力学学报,2001,33: 275~283
18 Niu Z R, Cheng C Z, Zhou H L, Hu Z J. Analytic formulations for calculating nearly singularintegrals in two-dimensional BEM. Engineering Analysis with Boundary Elements,2007, 31: 949~964
19 Zhou H L, Niu Z R, Cheng C Z, Guan Z W. Analytical integral algorithm applied to boundary layer effect and thin body effect in BEM for anisotropic potential problems.Comput. Struct, 2008, 86: 1656~1671
27 Zhang X S, Zhang X X. Exact integrations of two-dimensional high-order discontinuous boundary element ofelastostaticsproblems. Engng Anal Bound Elem, 2004, 28: 725~732
3/3 首页 上一页 1 2 3 |


