实际的防撞装置 ,所以一般情况下: ,所以一般情况下:
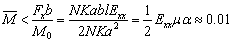 ,由图7不难看出: ,由图7不难看出: °论文网站。 °论文网站。
4、平动-转动联合作用下装置的弹性响应
任意作用在外箱梁上的外力,均可等价为通过椭圆中心的外力 和外扭矩 和外扭矩 ,使椭圆产生平动 ,使椭圆产生平动 ,转动 ,转动 。下面具体分析在平动-转动联合作用的下 。下面具体分析在平动-转动联合作用的下 和 和 关系。 关系。
当 , , , , 时,(7)式、(8)式过于复杂,所以选取和实际防撞装置接近的参数进行定性分析。一般情况下 时,(7)式、(8)式过于复杂,所以选取和实际防撞装置接近的参数进行定性分析。一般情况下 , , , , ,下面具体讨论在上述参数在取值范围的 ,下面具体讨论在上述参数在取值范围的 与 与 关系。 关系。
4.1、平动对于 的影响 的影响
 
图8为任意选取不同的 、 、 值,不同的无量纲位移下,无量纲扭矩与转角的关系。 值,不同的无量纲位移下,无量纲扭矩与转角的关系。
由图8中不难看出:位移对于 曲线取值,即转动的范围有较大影响;当 曲线取值,即转动的范围有较大影响;当 较大时,可以用纯转动下的 较大时,可以用纯转动下的 曲线近似代替存在平动时的 曲线近似代替存在平动时的 曲线 曲线
4.2、转动对 的影响 的影响
 
图9分布选取了 、 、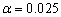 ,讨论 ,讨论 对于等效弹性系数的影响。 对于等效弹性系数的影响。
(1)、无量纲反力与无量纲位移 近似可以认为线性,其等效弹性系数与 近似可以认为线性,其等效弹性系数与 以及 以及 有关,随着 有关,随着 的增大,趋向于1; 的增大,趋向于1;
(2)、外箱梁旋转一定角度后,依然关于中心对称船撞桥墩,则 、 、 ;所以图9(a)只考察 ;所以图9(a)只考察 ,图9(b)只考察 ,图9(b)只考察 ; ;
(3)、由图9(a)可知, 曲线在 曲线在 左右出现极值,随着 左右出现极值,随着 的增大,极值逐渐减小。 的增大,极值逐渐减小。
(4)由图9(b)可知, 在第一象限时, 在第一象限时, 曲线在 曲线在 左右出现极值,随着 左右出现极值,随着 的增大,极值逐渐增大。当 的增大,极值逐渐增大。当 在第二象限时, 在第二象限时, 曲线除在 曲线除在 左右出现极值外,还在 左右出现极值外,还在 附近出现与 附近出现与 相反的极值,且随着 相反的极值,且随着 的增大,极值逐渐增大。 的增大,极值逐渐增大。
5、总结
分析了理想椭圆型桥墩防撞装置模型,计算刚性外箱梁在不同加载下的力—位移曲线和扭矩—转角曲线。
(1)、单纯平动下:长轴、短轴方向上力—位移曲线相互独立,无量纲位移小于0.5时,认为等效弹性系数为恒值,即力位移线性相关;需要平衡扭矩平衡装置,无量纲平衡扭矩在无量纲位移小于0.5时,近似为无量纲位移的二次方函数。
(2)、防撞装置实际转动角度远小于5°,无量纲扭矩近似为转角的三次方函数;随着 增大、 增大、 减小,装置越难转动。 减小,装置越难转动。
(3)、进一步定性的分析了外箱梁既发生转动又发生平动时,装置力—位移曲线与扭矩—转角曲线,即平动对扭矩—转角曲线的影响,转动对力—位移曲线的影响。
(4)、以 的椭圆型防撞装置为例,在已知外力与扭矩时,可以先求出扭转角度;利用图3曲线初步计算长、短轴上的位移,再根据图9迭代计算。可得到精度很高的 的椭圆型防撞装置为例,在已知外力与扭矩时,可以先求出扭转角度;利用图3曲线初步计算长、短轴上的位移,再根据图9迭代计算。可得到精度很高的 。或者在防撞装置最大允许变形、转动的条件下,亦可求得可承受的最大撞击力与其相应位置。 。或者在防撞装置最大允许变形、转动的条件下,亦可求得可承受的最大撞击力与其相应位置。
参考文献
[1]侯秀丽.桥梁工程重大坍塌事故调查与分析[D].中南大学硕士学位论文.2006
Hou Xiuli. Investigation and analysis on significantcollapsing accident for Bridge building [D]. Master Thesis. Central South University. 2006
4/4 首页 上一页 2 3 4 |


