 (5) (5)
弹簧对外箱梁的总扭矩为:
 (6) (6)
最终,外扭矩 表示为: 表示为:
 (7) (7)
(6)式、(7)式分别给出了外力 、外扭矩 、外扭矩 与外箱梁平动 与外箱梁平动 以及转角 以及转角 之间的关系,由此可进一步分析防撞装置的力学响应。 之间的关系,由此可进一步分析防撞装置的力学响应。
1.4、模型补充说明
1.4.1、 、 、 、 、 之间的制约关系 之间的制约关系
外箱梁在外力,外扭矩作用下,发生平动 ,转动角度 ,转动角度 后,必须保证任意一点都不与内箱梁发生碰撞,所以,在极坐标中,相同的极角下,外箱梁的极轴半径必须不小于内箱梁。 后,必须保证任意一点都不与内箱梁发生碰撞,所以,在极坐标中,相同的极角下,外箱梁的极轴半径必须不小于内箱梁。
 (8) (8)
(8)式要求在任意的 下都满足。 下都满足。
1.4.2、假设4的合理性
假设内外箱梁为椭圆型时,垂直于外箱梁连接内箱梁的弹簧长度为: ,则 ,则 与弹簧实际长度 与弹簧实际长度 的最大误差为: 的最大误差为: 。 。
 
图2是在不同的 、椭圆结构参数 、椭圆结构参数 与弹簧长度的最大误差, 与弹簧长度的最大误差, 。而由于桥墩尺寸导致实际的防撞装置 。而由于桥墩尺寸导致实际的防撞装置 , , 。所以实际防撞装置的尺寸误差约为 。所以实际防撞装置的尺寸误差约为 ,并且内箱梁是否为椭圆只与 ,并且内箱梁是否为椭圆只与 、 、 、 、 之间的取值范围有关,所以误差可以忽略,即认为垂直于外箱梁长度相同的弹簧连接的内箱梁为椭圆型。 之间的取值范围有关,所以误差可以忽略,即认为垂直于外箱梁长度相同的弹簧连接的内箱梁为椭圆型。
2、单纯平动力学性能分析
当 , , , , 时,由于椭圆并不是关于过椭圆中心的任意直线对称,所以 时,由于椭圆并不是关于过椭圆中心的任意直线对称,所以 不恒等于零,即在外力过椭圆中心时,需要外扭矩平衡。 不恒等于零,即在外力过椭圆中心时,需要外扭矩平衡。
2.1、无量纲化
引入无量纲化弹性反力 , , 、无量纲扭矩 、无量纲扭矩 和无量纲化位移 和无量纲化位移 、 、 ,无量纲参数 ,无量纲参数 分别为: 分别为:
 , ,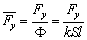 , , , , , , , , 船撞桥墩, 船撞桥墩, , , , , , ,
其中:特征长度 ,为装置的最大可能压缩量; ,为装置的最大可能压缩量;
特征反力: ,为装置内部所有弹簧并联、最大压缩量 ,为装置内部所有弹簧并联、最大压缩量 时的反力; 时的反力;
特征扭矩: ; ;
位移方向角: ,表示位移与 ,表示位移与 轴正方向夹角。 轴正方向夹角。
经过无量纲处理后可得:
 (9) (9)
 (10) (10)
其中: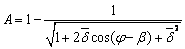

 , , 为外箱梁极坐标下的极角,与 为外箱梁极坐标下的极角,与 同象限。 同象限。
可见,经过无量纲化后模型的等效“力-位移”、“平衡扭矩-位移”曲线,只与外箱梁结构参数 有关,而与外箱梁具体尺寸 有关,而与外箱梁具体尺寸 、 、 无关,也与弹簧圈密度和弹性系数无关。该结论由模型本身的几何相似性确定。 无关,也与弹簧圈密度和弹性系数无关。该结论由模型本身的几何相似性确定。
2.2、力-位移关系
2.2.1、小变形下力—位移关系
当外箱梁位移很小,即 或 或 时,(9)式可以通过小参数展开,保留 时,(9)式可以通过小参数展开,保留 、 、 一次项,略去二次以上各项,简化为: 一次项,略去二次以上各项,简化为:
 (9-1) (9-1)
2/4 首页 上一页 1 2 3 4 下一页 尾页 |


