在具体计算式①—③时候,需要对行业进行界定。对此,经济学家还未形成共识,但是大多数并不认同行业分类越细越好。目前较为一致的做法是假定SITC 3位数或HS4位数分组定义为同一行业。在我国,对行业的划分与SITC2位数或HS2位数的划分非常接近。这种划分虽然包含的范围比较大,但是能使分析的结果更贴近我国的实际情况。因此,本文分别用HS2位数数据计算IIT,用HS4位数数据来分离HIIT和VIIT。[1]于是,我们可以得到关于上述四个指标在2009年的样本数据。在此基础上,把比较优势分为三类: 表示 表示 国在行业 国在行业 上具有较强的比较优势; 上具有较强的比较优势; 表示 表示 国在行业 国在行业 上具有较弱的比较优势; 上具有较弱的比较优势; 表示 表示 国在行业 国在行业 上不具有比较优势。与此同时,把贸易结构也分为三类: 上不具有比较优势。与此同时,把贸易结构也分为三类: 的贸易归为OWT, 的贸易归为OWT, 的贸易归为IIT。进一步以0.5为界,将IIT细分为HIIT和VIIT,即比值超过0.5的贸易归为HIIT,余下的部分归为VIIT。这样,按照比较优势和贸易结构这两个属性对96个观测数据进行分类,列出其频数表,即得到一张3×3的列联表(见表1)。 的贸易归为IIT。进一步以0.5为界,将IIT细分为HIIT和VIIT,即比值超过0.5的贸易归为HIIT,余下的部分归为VIIT。这样,按照比较优势和贸易结构这两个属性对96个观测数据进行分类,列出其频数表,即得到一张3×3的列联表(见表1)。
表1 比较优势和贸易结构分类频数表
|
比较优势 贸易结构
|
  
|
合计
|
|

|
12(18.3) 10(8.3) 18(13.3)
|
40
|
|

|
7(14.2) 10(6.5) 14(10.3)
|
31
|
|

|
25(11.5) 0(5.2) 0(5.2)
|
25
|
|
合计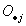
|
44 20 32
|
96
|
 在表1中,行和 在表1中,行和 ,该数据显示在贸易结构中,有44个行业的进出口贸易归为OWT,有32个行业的进出口贸易归为VIIT,还有20个行业的进出口贸易归为HIIT;列和 ,该数据显示在贸易结构中,有44个行业的进出口贸易归为OWT,有32个行业的进出口贸易归为VIIT,还有20个行业的进出口贸易归为HIIT;列和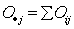 ,该数据显示不具有比较优势的行业数量最多,共有40个,其次是具有较弱比较优势的行业,共有31个;总和 ,该数据显示不具有比较优势的行业数量最多,共有40个,其次是具有较弱比较优势的行业,共有31个;总和 =96,即表示共对96个行业的数据进行分类统计。用列联表可检验比较优势是否与贸易结构有关。 =96,即表示共对96个行业的数据进行分类统计。用列联表可检验比较优势是否与贸易结构有关。 :比较优势与贸易结构独立; :比较优势与贸易结构独立; :比较优势与贸易结构不独立。在 :比较优势与贸易结构不独立。在 成立下,由样本估计的理论频数 成立下,由样本估计的理论频数 = = , , 1,2,3。用该式计算的各数据填入表1的括号内。在此基础上可求得分类资料 1,2,3。用该式计算的各数据填入表1的括号内。在此基础上可求得分类资料 统计量,即有 统计量,即有 =~ =~ 。将表1的数据代入,求得 。将表1的数据代入,求得 =40.6> =40.6> 。由此可知,比较优势对贸易结构的影响在 。由此可知,比较优势对贸易结构的影响在 下是高度显著的。在这里, 下是高度显著的。在这里, 检验只能说明行变量(比较优势)与列变量(商品贸易结构)存在相关关系国际贸易论文,并不能具体说明某行与某列有关联。对此,我们需要进一步通过对应分析来作出判断。 检验只能说明行变量(比较优势)与列变量(商品贸易结构)存在相关关系国际贸易论文,并不能具体说明某行与某列有关联。对此,我们需要进一步通过对应分析来作出判断。
三、比较优势和贸易结构的对应分析
1.对应分析的基本思想和步骤
对应分析(correspondenceanalysis)是一种在R型和Q型因子分析的基础上发展起来的多元统计分析方法。它的基本思想是将一个列联表中的频数矩阵进行适当的变换,使变换后的数据对行与对列是相对应的,从而可以同时对行和对列进行分析,以发现行列因素间的关系。
对应分析首先将表1的列联表转化为过渡矩阵 ,其中: ,其中:
 , , =1,2,3; =1,2,3; =1,2,3 =1,2,3
其次,计算矩阵 中各列间的协方差阵 中各列间的协方差阵 = = ,矩阵 ,矩阵 中各行间的协方差阵 中各行间的协方差阵 = =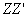 。由线性代数可知, 。由线性代数可知, 和 和 有完全相同的非零特征根,记作 有完全相同的非零特征根,记作 , , 。设 。设 为相对于特征根 为相对于特征根 的 的 的特征向量,则有 的特征向量,则有  。在该式两边左乘矩阵 。在该式两边左乘矩阵 得 得 ,即 ,即 。该式表明 。该式表明 为相对于特征值 为相对于特征值 的 的 的特征向量。这样, 的特征向量。这样, 和 和 相应的特征向量就有了密切的关系。 相应的特征向量就有了密切的关系。
若特征根累计百分比 ,则可确定因子个数为 ,则可确定因子个数为 (一般取 (一般取 =2)。将 =2)。将 的第1因子与第2因子及 的第1因子与第2因子及 的第1因子与第2因子同时绘在同一坐标轴上,建立对应分析图即可揭示不同类别的比较优势和不同类别的贸易结构间的关系。在对应分析图中,从二维坐标的(0,0)点出发,若代表行变量(比较优势)某个类别或等级的点,与代表列变量(贸易结构)某个类别或等级的点在同一方位上距离较近,则表明二者有较强的关联性;若距离较远或不在同一方位上,则表明二者关联性较弱或无关联性核心期刊目录。这是一般的 的第1因子与第2因子同时绘在同一坐标轴上,建立对应分析图即可揭示不同类别的比较优势和不同类别的贸易结构间的关系。在对应分析图中,从二维坐标的(0,0)点出发,若代表行变量(比较优势)某个类别或等级的点,与代表列变量(贸易结构)某个类别或等级的点在同一方位上距离较近,则表明二者有较强的关联性;若距离较远或不在同一方位上,则表明二者关联性较弱或无关联性核心期刊目录。这是一般的 检验和因子分析所不能作到的。 检验和因子分析所不能作到的。
2/3 首页 上一页 1 2 3 下一页 尾页 |


