论文摘要:解题时应时刻明确解题的最终目的是什么?能否运用各种手段直接达到目的?要尽量避免盲目推演而造成无益的循环运算。“设而不求”是解决这个问题的一个好方法。所谓设而不求,就是指在解题过程中根据需要设出变量,但是并不具体的去直接解出变量的值。它给解这一类题提供了较好的切入点和较少的运算量,不失为一好法.那么是什么原因导致设了未知数之后却不必要求出来呢?分析一下计算的过程,发现所求的问题与所设的未知数之间可以通过计算建立联系,从而无必要求未知数而得到了问题的答案,也就是“设”为基础,而“不求”是关键、是技巧,从而得到需要的结论。
论文关键词:设而不求,整体入手,灵活消去,转化方程,巧达目标,仅作桥梁,恒等变形
一、设而不求,整体代入
在解题过程中,往往有些步骤和环节并不是非有不可的,这些可称为“非必求成份”,解题时若能眼观全局,明确最终目的,从整体入手,直奔终点,巧妙地解开“非必求成份”,就能省时省力,获得巧解。
例1三棱锥的三个侧面互相垂直,它们的面积分别是6㎡、4㎡和3㎡。求它的体积。
 解析: 解析:
如图设三棱锥S-ABC的三条侧棱长分别为xm,ym,zm,则三个侧面积分别为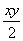 、 、 、 、 ,依题意有 ,依题意有 , ,
①×②×③后取算术平方根可得xyz=24.
而 = = = = () ()
例2已知椭圆 为焦点,点P为椭圆上一点, 为焦点,点P为椭圆上一点, ,求 ,求 。 。
解析:由题意知点P为椭圆上一点,根据椭圆的定义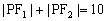 。 。
再注意到求 的关键是求出 的关键是求出 这一整体,则可采用如下设而不求的解法:设 这一整体,则可采用如下设而不求的解法:设
由椭圆定义得 ① ①
由余弦定理得 ② ②
①-②得, 
在这里不必分别求出x,y,z或 , , ,而是直达终点求出xyz或 ,而是直达终点求出xyz或 的值,这种把“xyz”作为“整体化”灵活处理“计算块”的做法却是省时省力。 的值,这种把“xyz”作为“整体化”灵活处理“计算块”的做法却是省时省力。
二、设而不求,灵活消去
在解题过程中,不解方程组,利用已知条件和方程的特点,灵活地进行等量代换而使问题获得解决,也能省时省力。
例3若A、B、C是曲线xy=1上的三点,证明: 的重心H必在此双曲线上。 的重心H必在此双曲线上。
证明:设A、B、C三点的坐标依次为 , , , , , ,
则 。于是AH的方程为: 。于是AH的方程为: …………① …………①
同理BH的方程为: …………② …………②
所以点H的坐标 同时满足①和②即 同时满足①和②即 …………③ …………③
 …………④ …………④
③×④得
化解整理得 ,显然 ,显然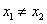 ,∴ ,∴
即表明 的重心H必在双曲线xy=1上。 的重心H必在双曲线xy=1上。
本题的关键是将③④两式相乘,从而推出 ,它避免了解二元一次方程组。由此可以看出,灵活消元的方法,常可以避免冗长的计算,既提高了解题速度又可减少差错。 ,它避免了解二元一次方程组。由此可以看出,灵活消元的方法,常可以避免冗长的计算,既提高了解题速度又可减少差错。
例4求过椭圆 内一点A(1,1)的弦PQ的中点M的轨迹方程。 内一点A(1,1)的弦PQ的中点M的轨迹方程。
解析:设动弦PQ的方程为 ,设P( ,设P( ),Q( ),Q( ),M( ),M( ),则: ),则: ① ① ② ②
①-②得:
当 时, 时,
由题意知 ,即 ,即 ③ ③
③式与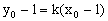 联立消去k,得 联立消去k,得 ④ ④
当 时,k不存在,此时, 时,k不存在,此时, ,也满足④。 ,也满足④。
故弦PQ的中点M的轨迹方程为: 。 。
注:通过将P、Q的坐标代入曲线方程,再将两式相减的过程,称为代点相减。这里,代点相减后,适当变形,出现弦PQ的斜率和中点坐标,是实现设而不求的关键。
三、设而不求,转化方程
有些数字等式的证明,若通过计算,十分繁杂,若设其等于x,而转化为对含未知数x的方程的研究,从而获得巧证。
例5证明
证明:设 , ,
则两边立方整理得 ,可化为 ,可化为 , ,
∵ 恒正,∴x-1=0即x=1∴ 恒正,∴x-1=0即x=1∴
设而不求,化等式证明为解方程问题,正巧特殊方程有唯一的实根x=1,从而证得原等式成立。
例6已知点P(3,4)为圆C: 内一点,圆周上有两动点A、B,当∠APB=90时,以AP、BP为邻边,作矩形APBQ,求顶点Q的轨迹方程。 内一点,圆周上有两动点A、B,当∠APB=90时,以AP、BP为邻边,作矩形APBQ,求顶点Q的轨迹方程。
解析:设A( ),B( ),B( ),Q(x,y) ),Q(x,y)
由题意得: ① ① ② ②
 ③ ③ ④ ④
 ,即 ,即 。⑤ 。⑤
 
将①②⑤代入上式并整理得 ,即为点Q的轨迹方程。 ,即为点Q的轨迹方程。
注:本题的目标是找到x、y所满足的方程,而逐步消去无关的 则是解答问题的关键。 则是解答问题的关键。
四、设而不求,巧达目标
解题过程中,时刻明确解题的最终目的,能否经巧妙运算,省去无益的循环运算,直达目标。
例7过圆外一点P(a,b),引圆 的两条切线,求经过两个切点的直线方程。 的两条切线,求经过两个切点的直线方程。
解析:设切点 和 和 则切线 则切线 ,切线 ,切线 ,可见 ,可见 和 和 都满足方程: 都满足方程: ,而次方程表示直线,故方程 ,而次方程表示直线,故方程 为过两切线的直线方程。 为过两切线的直线方程。
若先求出切点坐标,再求经过两个切点的直线方程,则情况复杂,计算量大。
例8抛物线的方程为y=4x,过P(1,2)作两条倾斜角互补的直线PA、PB交抛物线于A、B点,求AB的纵坐标之和及直线AB的斜率.
解析:设A(x,y),B(x,y).
(Ⅰ)略,y+y=-4;
(Ⅱ)由题意得:y=4x,故y-y=4(x—x),即==-1.
y=4x,∴直线AB的斜率为-1.
点评:此法的关键是通过两个函数式的相减运算,得到了斜率的形式,在双曲线和椭圆中还可得到中点的坐标形式,达到设而不求的目的.
五、设而不求,仅作桥梁
根据解题的需要,常引进一个量作为中间过度的桥梁,使问题获得解决。 1/2 1 2 下一页 尾页 |


