| 本文假设蜂窝微孔结构在连续介质中连续分布,微孔结构可以视为一种材料模式而非子结构。以蜂窝微结构的尺寸作为设计变量,单元内任意一点的尺寸变量r量插值得到,数学表达式为
 (6) (6)
式(6)中m为插值区域内尺寸变量的个数; 是插值函数。 是插值函数。
如图4所示,设物质点j具有紧支域 ,基于过滤方式的插值形函数表达式为 ,基于过滤方式的插值形函数表达式为
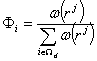 (7) (7)
其中
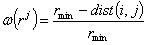 (8) (8)
或
 (9) (9)

图4物质点j及其支持域
Fig.4materialpointjanditssupportdomain
式中 ,r为过滤半径,其定义具有网格无关性;dist(i,j)为物质点i和j间的距离。式(8)-(9)中过滤半径值对应结构制造加工最小尺寸和最小孔洞。物质点变量确定是其本身及其预定义领域的有无,方法可称为物质点均匀化法,物质点均匀化法不仅能抑制棋盘格现象,还能进一步克服拓扑优化结果存在着大量多孔结构的缺点。 ,r为过滤半径,其定义具有网格无关性;dist(i,j)为物质点i和j间的距离。式(8)-(9)中过滤半径值对应结构制造加工最小尺寸和最小孔洞。物质点变量确定是其本身及其预定义领域的有无,方法可称为物质点均匀化法,物质点均匀化法不仅能抑制棋盘格现象,还能进一步克服拓扑优化结果存在着大量多孔结构的缺点。
3空间连续尺寸场的结构响应量与敏度推导
结构总刚度阵K、结构总质量阵M和结构总体积V表达式分别为
 (10) (10)
 (11) (11)
 (12) (12)
式中k,m和V分别表示单元刚度阵、单元质量阵和单元体积,M是单元总数。B是应变矩阵;D是弹性矩阵;N是插值矩阵。
在连续体结构拓扑优化中,结构响应量如固有特征值的敏度表达式归结为总刚度阵、总质量阵等的敏度表达式求解,根据复合函数链式求导法则,总刚度阵、总质量阵和总体积的敏度表达式分别为
 (13) (13)
 (14) (14)
 (15) (15)
4拓扑优化建模与求解
动态结构拓扑优化分为结构固有频率拓扑优化和动响应拓扑优化两类。结构固有频率拓扑优化通常以结构一阶特征值最大化为目标,体积比f为约束建立优化模型。在工程最常见的谐响应拓扑优化中,以区域内关心自由度振幅平方和最小化为目标,体积比f为约束建立优化模型。两类优化数学模型如式(16)~(17)所示。
  (16) (16)
  (17) (17)
式中 是结构一阶特征值;V和V分别表示优化后和初始结构体积; 是结构一阶特征值;V和V分别表示优化后和初始结构体积; 是结构特征值列阵; 是结构特征值列阵;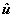 是各阶模态向量组成的模态矩阵。设计变量下限 是各阶模态向量组成的模态矩阵。设计变量下限 用于避免有限元分析的奇异性,这里取值 用于避免有限元分析的奇异性,这里取值 。当设计变量值为1时,由式(15)可得体积敏度敏度为0,为了避免优化求解的奇异性,设计变量上限取值 。当设计变量值为1时,由式(15)可得体积敏度敏度为0,为了避免优化求解的奇异性,设计变量上限取值 。在谐响应优化中,关心自由度振幅平方和 。在谐响应优化中,关心自由度振幅平方和 ,其中 ,其中 是复振幅u的共轭,L是关心自由度标识矩阵,当某自由度振幅为考察对象,矩阵L相应对角线元素值为1,其余元素为0; 是复振幅u的共轭,L是关心自由度标识矩阵,当某自由度振幅为考察对象,矩阵L相应对角线元素值为1,其余元素为0; 是激振圆频率;C是总阻尼阵;F是复载荷振幅列阵。 是激振圆频率;C是总阻尼阵;F是复载荷振幅列阵。
第j阶特征值 和关心自由度振幅平方和A的敏度表达式为 和关心自由度振幅平方和A的敏度表达式为
 (18) (18)
 (19) (19)
式中 是第j阶特征值位移向量, 是第j阶特征值位移向量, 表示“·”的实数部分,伴随向量满足伴随方程 表示“·”的实数部分,伴随向量满足伴随方程
 (20) (20)
设阻尼阵采用比例阻尼形式 ,阻尼系数 ,阻尼系数 和 和 为常数,则有 为常数,则有
 (21) (21)
在每轮优化迭代中,采用启发式算法更新微孔尺寸变量值,数学表达式为
 , ,
 式中上标k表示优化迭代步数,运动极限m(0m和阻尼系数 式中上标k表示优化迭代步数,运动极限m(0m和阻尼系数 用于保证优化迭代的稳健性,在动态拓扑优化问题中, 用于保证优化迭代的稳健性,在动态拓扑优化问题中, , , 是一种典型的取值。式中 是一种典型的取值。式中
 (22) (22)
其中F是目标函数;l是拉格朗日乘子,可通过满足体积函数二分法计算求得。优化迭代至尺寸变量相对变化率满足
 (23) (23)
5二维动态拓扑优化数值算例
本节采用二维动态拓扑优化算例对提出的方法进行验证。鉴于高阶等参元有利于抑制棋盘格现象,为了检验算法的有效性,这里采用四节点平面应力单元离散结构。各算例在Matlab2007中编程实现,采用50%体积比约束建立拓扑优化模型。在优化迭代终止后,根据式(5)计算密度值,并采用阈值0.5进行结果输出。
算例1如图5所示的短悬臂梁尺寸为3200mm×2000mm×1mm,左端面全支撑,右端面中点处有一质量大小为100kg的集中质量点,仅计垂直方向的惯性。结构离散为48×30个矩形单元,拓扑优化模型以一阶固有特征值最大化为目标。当采用SIMP插值的单元变密度法进行优化,出现局部模态现象,导致优化迭代不收敛。当采用48×30个均匀和随机两种不同尺寸场描述拓扑结构时,本文方法分别优化迭代至50步和53步收敛,两种不同尺寸场分布下的最优拓扑结果如图6所示,一阶固有频率优化迭代历程如图7所示。当结构分别离散为32×20和64×40个矩形单元,最优拓扑结果如图8所示。

图5短悬臂梁
Fig.5shortcantileverbeam

(a)均匀分布

(b)随机分布
图6不同尺寸场分布下的拓扑优化结果对比
Fig.6comparisonofoptimumtopologywithdifferentsizefield

图7一阶固有频率优化迭代历程
Fig.7Historycurveofthefirstorderfrequency

(a)32×20

(b)64×40
图8不同离散网格和对应尺寸场下的拓扑优化结果对比
Fig.8comparisonofoptimumtopologywithdifferentgirdandsizefield
由结果可知,两种不同尺寸场分布下的拓扑优化结果均未出现类似棋盘格的散乱点现象。 2/3 首页 上一页 1 2 3 下一页 尾页 |


