论文导读::研究了由径向横观各向同性不可压缩的neo-Hookean材料组成的圆柱形管在翻转后的有限变形问题。利用材料的不可压缩条件和半逆解法对相应的数学模型进行求解,并根据边界条件得到了翻转后的圆柱形管的内半径以及轴向伸长率应满足的非线性方程组。通过数值算例讨论了材料参数和结构参数对翻转后圆柱形管的内半径以及轴向伸长率变化的影响。结果表明:初始厚度对翻转后圆柱形管的内半径与轴向伸长率没有本质上的影响;而径向各向异性参数却有本质上的影响,特别是在轴向伸长率方面。
论文关键词:横观各向同性,超弹性圆柱管,翻转,轴向伸长率
1. 引言
众所周知,以橡胶材料和类橡胶材料为主要的超弹性材料在机械工程、石油化工、航空航天等领域的应用非常广泛。更重要的是,其材料特性和几何特性都具有典型的非线性性质。而超弹性材料构成的圆柱管的翻转问题的理论和实验研究众多专家和学者关注的焦点。
Rivlin[1]首先研究了Mooney-Rivlin材料构成的圆柱形管的翻转问题。作者在文中假设了翻转后的形状仍然是圆柱形,并且翻转后的圆柱管的表面处于无约束状态,端部合力为零,最后在理论上证明了翻转后仍为圆柱形的结论。后来,Varga[2]得到大量具有不同几何特性的圆柱管翻转的实验结果。这些实验结果为:翻转后的形状都接近于端部略有扭曲的圆柱形,且扭曲只在端部区域。文献[1]的理论结果和文献[2]的实验结果表明除去端部,理论解和实际解非常接近。
此后,Chadwick和Haddon[3]研究了一系列由Ogden[4]材料构成的圆柱形管的翻转问题。论文主要研究了翻转后圆柱形解的存在和唯一性。Chadwick[5]理论上证明了所有的Mooney-Rivlin材料翻转后圆柱形解存在且唯一论文开题报告范文。Adeleke[6]推广了Chadwick关于存在性和唯一性的结论物理论文,证明了对于由Truesdell和Noll[7]提出的满足 -不等式的所有材料的翻转后圆柱形解存在且唯一。关于圆柱形管其它类型的有限变形问题还可参见文献[8~11]。 -不等式的所有材料的翻转后圆柱形解存在且唯一。关于圆柱形管其它类型的有限变形问题还可参见文献[8~11]。
本文主要研究由径向横观各向同性neo-Hookean材料组成的不可压缩超弹性圆柱管形翻转后的状态。论文首先基于非线性弹性力学的有限变形理论建立了相应问题的数学模型,并求得了描述翻转后的圆柱形管的内半径以及轴向伸长率应满足的非线性方程组。最后通过数值算例分析了材料参数和结构参数对翻转后的圆柱管有限变形的影响。
2. 数学模型及求解
对于由不可压缩超弹性材料构成的无限长圆柱形管,假设其变形前的构形为
![速度翻转后的不可压缩neo-Hookean圆柱管的有限变形[1] 翻转](/d/file/picture/201304/03/19.files/image002.gif) 。(1) 。(1)
将圆管翻转,在径向对称变形的假设下,可得其变形后的构形为
![速度翻转后的不可压缩neo-Hookean圆柱管的有限变形[1] 翻转](/d/file/picture/201304/03/19.files/image003.gif) , (2) , (2)
注意到 对应映射到 对应映射到 , , 对应映射到 对应映射到 。由于变形是关于径向对称的,则有 。由于变形是关于径向对称的,则有
![速度翻转后的不可压缩neo-Hookean圆柱管的有限变形[1] 翻转](/d/file/picture/201304/03/19.files/image008.gif) ,(3) ,(3)
其中 是轴向伸长率。对应于式(3)的变形梯度张量为 是轴向伸长率。对应于式(3)的变形梯度张量为
 ,(4) ,(4)
主伸长为
 。(5) 。(5)
由材料的不可压缩性可知 ,即 ,即 ,因此有 ,因此有
 ,(6) ,(6)
易见,式(6)精确描述了翻转后的柱形管的轴向伸长率和半径之间的关系。
对应于不可压缩超弹性材料的Cauchy应力张量的主值为
 ,(7) ,(7)
其中 为不可压缩超弹性材料的应变能函数, 为不可压缩超弹性材料的应变能函数, 是静水压力。 是静水压力。
在径向对称变形的假设下,描述圆管翻转后变形构形的平衡微分方程可约化为
 。 (8) 。 (8)
由于翻转后的薄壁圆柱管的内、外表面是无约束的,因此有如下的边界条件
 。(9) 。(9)
根据文献[1]的假设,即假设在端部给定合力 ,可以得到近似平均的端部条件 ,可以得到近似平均的端部条件
 。(10) 。(10)
利用式(7),(9)1物理论文,对式(7)积分得
 。 (11) 。 (11)
由表面不受力条件(9)2,得
 。 (12) 。 (12)
其中 可由令式(6)中 可由令式(6)中 得到,即 得到,即 。 。
利用分部积分法和式(12),平均端部条件(10)变为
 。 (13) 。 (13)
本文中,考虑柱形管是由经典的径向横观各向同性的不可压缩neo-Hookean材料模型构成的,材料所对应的应变能函数 的形式为[10] 的形式为[10]
 ,(14) ,(14)
其中 为无穷小变形的剪切模量; 为无穷小变形的剪切模量; 是一个无量纲的材料参数,它描述了材料关于径向各向异性的程度。易见,若 是一个无量纲的材料参数,它描述了材料关于径向各向异性的程度。易见,若 ,则对应于各向同性neo-Hookean材料模型。 ,则对应于各向同性neo-Hookean材料模型。
将应变能函数(14)代入式(12)和(13),得到
 ,(15) ,(15)
 。(16) 。(16)
为了便于后面的讨论,引入如下无量纲的记号:
 , , ,(17) ,(17)
可以得到 论文开题报告范文。此外,将式(6)记为 论文开题报告范文。此外,将式(6)记为 ,然后令 ,然后令
 ,(18) ,(18)
从而可得
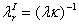 , , , , , ,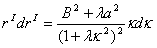 。(19) 。(19)
从而方程(15)和(16)的无量纲化方程为
 物理论文,(20) 物理论文,(20)
 。(21) 。(21)
1/2 1 2 下一页 尾页 |


