关于天体的计算_物理论文

论文导读:：关于天体的计算，物理论文。
论文关键词：关于天体的计算
 

关于天体的计算，我们可以归纳出这样几种典型问题：1．重力加速度的计算；2．中心天体质量的计算；3．第一宇宙速度的计算；4．中心天体密度的计算；5．周期与时间计算。

例题解读

1．重力加速度

例1．宇航员在地球表面以一定初速度竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度竖直上抛同一小球，需经过时间5t小球落回原处。（取地球表面重力加速度g＝10 m/s²，空气阻力不计）

⑴求该星球表面附近的重力加速度g^/；

⑵已知该星球的半径与地球半径之比为R_星:R_地＝1:4物理论文，求该星球的质量与地球质量之比M_星:M_地。

解析：⑴

所以有：

⑵，所以

可解得：M_星:M_地＝1′1²:5′4²＝1:80，

点拨：重力加速度的计算，我们一般这样处理论文提纲怎么写。由得，式中R为中心天体的半径，h为物体距中心天体表面的高度。

2．质量

例2．两个星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R，其运动周期为T，求两星的总质量。

解析：此为天体运动的双星问题，除两星间的作用外物理论文，其他天体对其不产生影响。

两星球周期相同，有共同的圆心，且间距不变，其空间分布如图2所示。

图2

设两星质量分别为M₁和M₂，都绕连线上O点做周期为T的圆周运动，两星到圆心的距离分别为L₁和L₂，由于万有引力提供向心力，

故有 =M ₁ ①

=M ₂ ②

由几何关系知 L₁+L₂=R， ③

联立解得 M₁+M₂=

点拨：天体质量的计算，我们的一般过程是这样的。1．由得；2．由得.

本题的解答告诉我们，物体在中心天体表面或表面附近时物理论文，物体所受重力近似等于万有引力。该式给出了中心天体质量、半径及其表面附近的重力加速度之间的关系，是一个非常有用的代换式。

3．第一宇宙速度

例3．若取地球的第一宇宙速度为8 km/s，某行星的质量是地球的6倍，半径是地球的1.5倍，这行星的第一宇宙速度约为 （ ）

A.16 km/s B.32 km/s

C.4 km/s D.2 km/s

解析： 此类题要结合第一宇宙速度的计算公式进行对比分析来计算.

由G=m得v=.

因为行星的质量M′是地球质量M的6倍，半径R′是地球半径R的1.5倍.即M′=6M，R′=1.5R得：

=2

即：v′=2v=2×8 km/s=16 km/s.答案为A.

点拨：计算第一宇宙速度有两种方法：1．由G=得：v=；2．由mg=m得：v=论文提纲怎么写。

4．密度

例4.中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T＝。问该中子星的最小密度应是多少才能维持该星体的稳定，不致因自转而瓦解。计算时星体可视为均匀球体。（引力常数G＝6.67×10^－11m3／kg·s²)

解析：考虑中子星赤道处一小块物质，只有当它受到的万有引力大于或等于它随星体一起旋转所需的向心力时物理论文，中子星才不会瓦解。

设中子星的密度为ρ，质量为M，半径为R，自转角速度为ω，位于赤道处的小块物质质量为m，则有

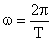
由以上各式得

代人数据解得

点拨：计算天体密度时，我们要注意下面的两个过程：1．由和得；2．由 和得。

5.周期

例5．神舟五号载人飞船在绕地球飞行的第5圈进行变轨，由原来的椭圆轨道变为距地面高度km的圆形轨道。已知地球半径km，地面处的重力加速度。试导出飞船在上述圆轨道上运行的周期T的公式（用h、R、g表示），然后计算周期T的数值（保留两位有效数字）

设地球质量为M，飞船质量为m物理论文，速度为v，圆轨道的半径为r，由万有引力和牛顿第二定律，有

地面附近

由已知条件

解以上各式得

代入数值，得

论文提纲怎么写。

例6．我国发射的“嫦娥一号”探月卫星沿近似于圆形轨道绕月飞行。为了获得月球表面全貌的信息，让卫星轨道平面缓慢变化。卫星将获得的信息持续用微波信号发回地球。设地球和月球的质量分别为M和m，地球和月球的半径分别为R和R₁，月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r₁，月球绕地球转动的周期为T。假定在卫星绕月运行的一个周期内卫星轨道平面与地月连心线共面，求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间（用M、m、R、R₁、r、r₁和T表示，忽略月球绕地球转动对遮挡时间的影响）。

解析：如图3所示：

　??

 1/2    1 2 下一页 尾页