用某一标量势来描述上式的右边是很困难的论文下载。由于 、 、 有特殊的依赖关系。我们用 有特殊的依赖关系。我们用 来表示是为了强调 来表示是为了强调 项与式(1)、(2)中的 项与式(1)、(2)中的 对应,从式(13)、(14)可推出二成分BEC。压强梯度 对应,从式(13)、(14)可推出二成分BEC。压强梯度 在二分量中沿相同的方向,然而 在二分量中沿相同的方向,然而 沿相反的方向。这种性质与4He超流体的二流体模型十分类似。 沿相反的方向。这种性质与4He超流体的二流体模型十分类似。
3 二分量BEC中的第一声波和第二声波
在此,我们将从二成分BES的四元方程组中推导出两个波模。在这里假设超流速度
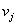 很小且非线性项可以忽略。由方程 很小且非线性项可以忽略。由方程 ,方程 ,方程 可得, 可得,
 (15) (15)
 (16) (16)
 (17) (17)
 (18) (18)
其中 , , 二流体模型, 第一声波为二成分中 二流体模型, 第一声波为二成分中 的振动,第二声波为 的振动,第二声波为 的振动。我们假定 的振动。我们假定 、 、 的振动分别和第一声波、第二声波相对应。现在式(17)、(18)中右边分别是 的振动分别和第一声波、第二声波相对应。现在式(17)、(18)中右边分别是 和 和 。可把 。可把 、 、 写成 写成 、 、 的函数形式, 的函数形式,
 (19) (19)
 (20) (20)
其中, , ,
 , ,


从方程(15)-(18)可导出两个波动方程,
 (21) (21)
 (22) (22)
考虑到平面波 , , 在平衡位置 在平衡位置 , , 附近以频率 附近以频率 、波矢 、波矢 的波动形式传播, 的波动形式传播,


波速为
 (23) (23)
其中 ,可通过长波极限下二流体模型,双成分BEC的Bogoliubov激子的色散关系得到。超流体4He的第一声波、第二声波的波模是 ,可通过长波极限下二流体模型,双成分BEC的Bogoliubov激子的色散关系得到。超流体4He的第一声波、第二声波的波模是 、 、 的独立振动。然而方程(23)不能描述第一声波、第二声波。因为这两个声波是混合在一起的论文下载。我们发现当 的独立振动。然而方程(23)不能描述第一声波、第二声波。因为这两个声波是混合在一起的论文下载。我们发现当 、 、 消失时 消失时 、 、 是独立振动的。此条件可简写为, 是独立振动的。此条件可简写为,


这两种波模的波速为
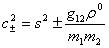 (24) (24)
其中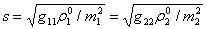 且 且 。 。 对应于 对应于 ,是第一声波, ,是第一声波, 对应于 对应于 ,是第二声波。第一声波波速随 ,是第二声波。第一声波波速随 增加而增加,第二声波波速随 增加而增加,第二声波波速随 增加而减小。当 增加而减小。当 时, 时, 变为虚数。这将导致流体力学框架坍塌,或在二分量BEC中出现相变。 变为虚数。这将导致流体力学框架坍塌,或在二分量BEC中出现相变。
4 总结
从耦合GP方程出发,我们用二流体模型的公式表示二分量BEC。此模型与4He超流体中的二流体模型吻合的非常好,得到的两个声模在4He超流体中是完全独立存在的。我们更感兴趣的是第二声模如何与二分量BEC中涡旋发生作用。
参考文献
[1]P. L. Kapitza, Nature 141, 74(1937).
[2]L. Tisza, Nature 141, 913(1938).
[3]L. Landau, J. Phys. U.S.S.R. 5,71 (1941).
[4]H. Takeuchi, N. Suzuki, K. Kasamatsu,H. Saito, and M. Tsubota, Phys. Rev.
B 81,094517 (2010).
2/2 首页 上一页 1 2 |


