论文导读::客观性是连续介质力学。因此将其称为两点张量。并明确指出变形梯度是客观性张量。考虑到功共轭也存在相似的问题。
论文关键词:客观性,一点张量,两点张量,变形梯度,功共轭
1简介
客观性是连续介质力学,特别是连续固体介质力学中重要的一个概念,它强调了本构关系与刚体转动无关。所谓客观性,也称为标架不变性、标架无差异,是指材料的本构关系不因观察者不同而发生形式上的变化,这就要求构建本构关系的应力应变张量在时空变换时遵守一定的准则以保证本构方程的标架不变性,即要求应力应变张量具有客观性。
变形梯度是一个联系初始构型与当前构型的两点张量,在连续介质力学中具有核心地位、是定义各类应变张量的基础,同时两点张量,基于变形梯度张量也可实现各类应力张量之间的转换。由于在构建本构关系时直接应用的是应变(应力)及与其共轭的应力(应变),必须鉴别各类应力应变量的客观性,因此现有文献与教材对各类应力应变讨论较多,且对基于一点的应力应变张量的客观性的具有统一的观点[1-4]。但对于变形梯度等两点张量的客观性的表述存在分歧,如匡震邦[3]与Belytschko等[4]对Euler-Lagrange两点张量的客观性给出了定义,并明确指出变形梯度是客观性张量,而黄克智[2]与Bock等[5]则认为变形梯度张量不是客观张量。这种表述上的分歧在于张量客观性的定义不同,那么到底该如何理解张量的客观性?为此本文从变形梯度张量的定义及张量分类开始,然后介绍客观性的几种定义,并基于连续介质力学中张量的逆及功共轭角度分析了几种定义的差别论文参考文献格式。
2变形梯度张量及张量的类型
这里仅以欧式空间为例,考虑变形体在固定参考构形内质点 的位置向量以 的位置向量以 表示, 表示, 时刻当前构形的同一物质点的位置向量以 时刻当前构形的同一物质点的位置向量以 表示,则变形体的运动可通过如下映射描述[6] 表示,则变形体的运动可通过如下映射描述[6]
 (1) (1)
对于同一物质点, 不随时间变化,称为物质坐标或Lagrange坐标,而 不随时间变化,称为物质坐标或Lagrange坐标,而 是同一物质点在 是同一物质点在 的空间位置,称为空间坐标或者Euler坐标。则变形梯度 的空间位置,称为空间坐标或者Euler坐标。则变形梯度 可表示为: 可表示为:
 (2) (2)
式(2)表示变形梯度将固定参考构形中 点邻域的有向线元 点邻域的有向线元 线性变换到当前构形中 线性变换到当前构形中 点邻域内有向线元 点邻域内有向线元 [1]。也就是 [1]。也就是 关系到固定参考构形与当前构形,因此将其称为两点张量。基于极分解定理变形梯度可表示为 关系到固定参考构形与当前构形,因此将其称为两点张量。基于极分解定理变形梯度可表示为
 (3) (3)
式中 为对称正定张量,分别称为右拉伸张量和左拉伸张量两点张量, 为对称正定张量,分别称为右拉伸张量和左拉伸张量两点张量, 为转动张量,其满足正交性条件。依据谱分解, 为转动张量,其满足正交性条件。依据谱分解, 可分别表示为 可分别表示为
 ; ; (4ab) (4ab)
其中 为 为 的特征值或主值,也称为主长度比, 的特征值或主值,也称为主长度比, 与 与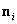 分别为Lagrange主方向与Euler主方向,且二者存在如下关系 分别为Lagrange主方向与Euler主方向,且二者存在如下关系
 (5) (5)
由此变形梯度可写为
 (6) (6)
式(6)明确表示了变形梯度与Euler主方向(坐标)及Lagrange主方向(坐标)的关系,因此将其称为Euler-Lagrange张量。而式(4)表明 仅与Lagrange坐标相关,称为Lagrange张量,同理则 仅与Lagrange坐标相关,称为Lagrange张量,同理则 为Euler张量。与Euler-Lagrange张量相对应还存在Lagrange-Euler两点张量,如变形梯度的逆 为Euler张量。与Euler-Lagrange张量相对应还存在Lagrange-Euler两点张量,如变形梯度的逆 可写为 可写为
 (7) (7)
其为Lagrange-Euler张量。综上可知,在连续介质力学中可将二阶张量按其与有向线元的关系[1,2]分为Lagrange张量,Euler张量,Euler-Lagrange张量,Lagrange-Euler张量四个类型。以下我们将注意到张量客观性的定义与张量的类型密切相关。
2客观性的定义
假定存在满足如下关系的两个时空坐标系
 ; ; (8) (8)
其中 , , 分为为正交张量和向量, 分为为正交张量和向量, 为常数。客观性原理认为材料的本构关系在式(8)的变换下保持形式不变,由此要求本构关系中的张量应为客观性张量。 为常数。客观性原理认为材料的本构关系在式(8)的变换下保持形式不变,由此要求本构关系中的张量应为客观性张量。
2.1张量的Truesdell客观性与Hill客观性及讨论
张量的第一种客观性定义是由Truesdell和Noll给出的[7],即对任意二阶张量 两点张量,若其在式(8)变换时,满足下式 两点张量,若其在式(8)变换时,满足下式
 (9) (9)
则称其为客观性张量。
必须说明文献[2、9、10]及文献[1、3、4]虽都给出了Truesdell客观性的定义,但其内涵是不同的,文献[2、9、10]中Truesdell客观性的定义域是全体张量,文献[1、3、4]中则明确认为Truesdell客观性仅对Euler一点张量而定义论文参考文献格式。存在类似差别还有Hill客观性[8]的定义,即文献[1、3、4]明确指出了Hill客观性是对Lagrange张量而定义的,即对任意Lagrange张量 ,如果在式(8)变换时,满足 ,如果在式(8)变换时,满足
1/2 1 2 下一页 尾页 |


