
如图2所示瞬态模型,其中X、Y、Z为运动坐标系下的坐标,x、y、z为静止坐标系下的坐标。在静止坐标系下,运动涡流场方程的位函数表述为
 (7) (7)
 (8) (8)
在运动坐标系下,运动涡流场方程的位函数表述为
 (9) (9)
 (10) (10)
显然在静止坐标系描述下,方程组矩阵由于速度项的存在而不对称,但运动坐标系描述下可保证方程组矩阵的对称性。尤其在感应线圈炮中应用,线圈炮的电枢在通过线圈时的加速过程,此时一般需要根据运动调整不同材料网格的相对位置,并对该过程进行瞬态场计算,采用固定在网格上的运动坐标系来描述问题自然更加方便。此时,方程中将不显式地出现 ,而速度反映在运动体的离散网格在每一时间步的位移中。 ,而速度反映在运动体的离散网格在每一时间步的位移中。
为了方便起见,把(1)和(3)式统一为:
 (11) (11)
当忽略源电流区中的涡流时,电流密度 和驱动线圈的电流I有如下关系: 和驱动线圈的电流I有如下关系:
 (12) (12)
式中  ——驱动线圈的截面积; ——驱动线圈的截面积;
 ——驱动线圈匝数; ——驱动线圈匝数;
 ——驱动线圈切向的单位矢量。 ——驱动线圈切向的单位矢量。
为保持系数矩阵的对称性,引入函数 瞬态模型,使 瞬态模型,使
 (13) (13)
把式(12)和式(13)代入式(11),得
 (14) (14)
在运动坐标系中利用加权余量对式(14)进行离散,把整个求解区域划分为M个单元,在任一单元e内,矢量磁位 的插值函数可用该单元各节点处的磁位近似表示为: 的插值函数可用该单元各节点处的磁位近似表示为:
 , ,
迦辽金形式的加权余量法以形状函数为权函数,在边值问题中,边界 上 上 ,边界 ,边界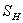 上 上 ,这是两个第一类边界条件。在有限元离散化方程建立以后,它们应作为强加边界条件来处理论文格式范文。对于余量的加权积分,在位函数已知的节点上,权函数应取为零,这样才能保证离散化方程组的方程数与未知数的个数相等,因此瞬态模型,作为权函数的形状函数在 ,这是两个第一类边界条件。在有限元离散化方程建立以后,它们应作为强加边界条件来处理论文格式范文。对于余量的加权积分,在位函数已知的节点上,权函数应取为零,这样才能保证离散化方程组的方程数与未知数的个数相等,因此瞬态模型,作为权函数的形状函数在 和 和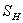 上应满足: 上应满足:

上式中形状函数的下标j代表节点号。分别在边界 、 、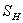 上取值。 上取值。
在驱动线圈和电枢区域V内以 为权函数,对式(14)作加权积分,并令其为零,得: 为权函数,对式(14)作加权积分,并令其为零,得:
 (15) (15)
运用矢量运算恒等式和矢量的积分变换公式,整理式(15)可得:
 (16) (16)
同理在运动坐标系下对(2)进行加权积分,并令其等于零,得:
 (17) (17)
利用高斯定理并结合边界条件整理得:
 (18) (18)
从式(16)和式(18)直接得出的离散化方程组,写成矩阵形式,可得:
 (19) (19)
以式(19)第一式为例进行单元分析,即
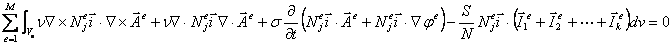 (20) (20)
 (21) (21)
式中各项:
 , , , ,
 (22) (22)
 (23) (23)
 (24) (24)
把(22)、(23)、(24)代入(20)得:
 (25) (25)
同理整理可得:
 (26) (26)
 (27) (27)
同理对式(19)第二式进行单元分析,整理得:



式(19)式第三式单元分析,得



同理对式(21)进行单元分析,得:

 把以上式子代入式(19)并整理得出单元平衡方程: 把以上式子代入式(19)并整理得出单元平衡方程:

并由此得出总系统的求解方程:
 (28) (28)
4、多级感应线圈炮的电路方程
多级同步感应线圈炮的等效电路模型如图3所示。其中每一个耦合电路代表线圈炮的一级。
可写出其第k级放电时电路方程为:
 (29) (29)
 ; ; ; ; ; ; ; ;
电磁场方程和连接的电路方程相接口的中间环节驱动线圈和电枢中的电流及感应电势。其中瞬态模型,电流是整个求解系统得独立状态变量,而感应电势则是矢量磁位的函数,是非独立状态变量。因而整个场路方程耦合求解的关键是感应电动势e。有限元区的感应电动势可通过与绕组所交链的磁通的变化来求得。假设电流只有x、y方向分量,z方向分量等于零, 为电流方向与x方向的夹角,且驱动线圈划分了P个单元,则由此可得每一级驱动线圈的感应电动势为: 为电流方向与x方向的夹角,且驱动线圈划分了P个单元,则由此可得每一级驱动线圈的感应电动势为:
2/3 首页 上一页 1 2 3 下一页 尾页 |


