论文导读::本文采用动态金茨堡-朗道(DGL)方程研究了薄膜厚度与错配应变对 取向单畴外延 取向单畴外延 (PTO)铁电薄膜相结构与稳定性的影响。结合平面内松弛应变(等效应变)、表面效应与退极化场等机电耦合边界条件,通过数值求解DGL方程获得外延单畴铁电薄膜错配应变—厚度相图和错配应变—温度相图。数值分析结果显示,由于生成的界面位错松弛了薄膜内错配应变,在理论高应变区相图与传统分析结果有较大差别,文中首次发现在理论高拉应力区会出现稳定的四方相(c相)结构,而单斜相(r相)结构能稳定的存在于较广的错配拉应变区。结果也显示,随着薄膜厚度的减小,表面效应与退极化效应会把顺电相扩展到更低温度区域,从而压缩稳定的铁电相存在的温度区域。 (PTO)铁电薄膜相结构与稳定性的影响。结合平面内松弛应变(等效应变)、表面效应与退极化场等机电耦合边界条件,通过数值求解DGL方程获得外延单畴铁电薄膜错配应变—厚度相图和错配应变—温度相图。数值分析结果显示,由于生成的界面位错松弛了薄膜内错配应变,在理论高应变区相图与传统分析结果有较大差别,文中首次发现在理论高拉应力区会出现稳定的四方相(c相)结构,而单斜相(r相)结构能稳定的存在于较广的错配拉应变区。结果也显示,随着薄膜厚度的减小,表面效应与退极化效应会把顺电相扩展到更低温度区域,从而压缩稳定的铁电相存在的温度区域。
论文关键词:金茨堡-朗道方程,铁电相图,尺寸效应,松弛应变
外延生长于基体上的铁电薄膜具有优异的物理性能,被广泛应用于微电子领域,成为非易失存储器、场效应管和热电传感器等的主要材料[1-2]。由于与基体材料晶格不匹配,薄膜内会产生错配应变(或内应力),其显著改变铁电薄膜的相变温度,相结构类型与相稳定性、铁电性能等[3-7],因此对错配应变—厚度相图与错配应变—温度相图的研究受到越来越多的关注。
本文提出了结合等效薄膜内应变(内应力)、薄膜表面晶格变化引起的极化改变和表面电荷引起的退极化效应等机电耦合边界条件,应用动态金茨堡-朗道方程,系统分析单畴外延PTO铁电薄膜相变稳定性和相结构的尺寸效应。错配应变-温度相图结果显示,在理论错配高应变区,松弛(真实)应变会降低铁电畴相稳定的温度,在一定薄膜厚度范围内,在拉应变区也能存在稳定的c相,对于单畴外延铁电薄膜还未见此类结果的报道。数值分析结果也显示,表面效应和退极化效应导致铁电相在更低温下稳定,并且随着薄膜厚度的减小尺寸效应,影响更显著。错配应变-厚度相图显示,随着温度的升高,r相的范围减小。在室温下,对一定厚度的铁电薄膜,在更广的拉应变范围内存在稳定的r相。因此,我们的结果可以在一定程度上指导在实验中选择合适参数以获得更优质铁电性能的单畴外延铁电薄膜核心期刊目录。
1 铁电薄膜理论分析
本文考虑 取向的单畴外延钙钛矿型PTO铁电薄膜生长在 取向的单畴外延钙钛矿型PTO铁电薄膜生长在 取向的立方晶体基体上,定义直角坐标系: 取向的立方晶体基体上,定义直角坐标系: ,薄膜平面为 ,薄膜平面为 平面, 平面, 轴沿薄膜厚度方向,坐标原点位于薄膜的中心,薄膜厚度为 轴沿薄膜厚度方向,坐标原点位于薄膜的中心,薄膜厚度为 。当钙钛矿型铁电薄膜对称夹持在两电极层中间时,铁电材料广义朗道-德文希尔-金茨堡相变自由能可以表示为[6,7,12]: 。当钙钛矿型铁电薄膜对称夹持在两电极层中间时,铁电材料广义朗道-德文希尔-金茨堡相变自由能可以表示为[6,7,12]:
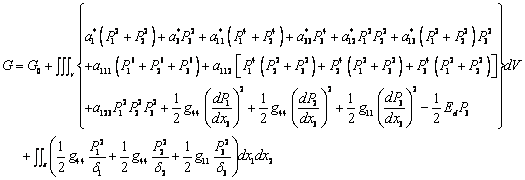 (1) (1)
其中 是各个坐标方向的极化强度, 是各个坐标方向的极化强度, 是电致伸缩系数, 是电致伸缩系数, 是金茨堡系数, 是金茨堡系数, 分别为考虑薄膜与基体晶格错配应力,基体对相变约束等影响的材料介电系数和高阶介电系数,可表示为[7,12]: 分别为考虑薄膜与基体晶格错配应力,基体对相变约束等影响的材料介电系数和高阶介电系数,可表示为[7,12]:
 , , , , , ,
 , , , ,
 ,(2) ,(2)
其中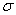 为薄膜内真实平面应力, 为薄膜内真实平面应力, 是材料柔性系数, 是材料柔性系数, 是材料的介电系数,其中 是材料的介电系数,其中 , , 分别为铁电材料块体的居里温度和居里常数。公式(1)右端体积分式包含块体材料自由能、弹性能、电场能和极化梯度能,面积分包含上下表面(界面)上极化强度松弛引起的能量改变。其中 分别为铁电材料块体的居里温度和居里常数。公式(1)右端体积分式包含块体材料自由能、弹性能、电场能和极化梯度能,面积分包含上下表面(界面)上极化强度松弛引起的能量改变。其中 和 和 分别表征薄膜表面三个方向极化值改变的外延长度[6,13,14],它是唯象的物理量。假设薄膜平面尺寸远大于厚度,本文只考虑极化强度在厚度方向的梯度,极化强度在水平方向的梯度 ?Pi/?x1,?Pi/?x2不予考虑。公式(1)右端体积分中包含薄膜内的退极化电场 分别表征薄膜表面三个方向极化值改变的外延长度[6,13,14],它是唯象的物理量。假设薄膜平面尺寸远大于厚度,本文只考虑极化强度在厚度方向的梯度,极化强度在水平方向的梯度 ?Pi/?x1,?Pi/?x2不予考虑。公式(1)右端体积分中包含薄膜内的退极化电场 。考虑到实际表面电极与铁电薄膜材料之间的缺陷会减小电荷补偿效应尺寸效应,改变薄膜内的退极化场,因此适合采用如下退极化电场的表达式[15,16] 。考虑到实际表面电极与铁电薄膜材料之间的缺陷会减小电荷补偿效应尺寸效应,改变薄膜内的退极化场,因此适合采用如下退极化电场的表达式[15,16]
 (3) (3)
其中 和 和 分别为真空和电极材料介电系数, 分别为真空和电极材料介电系数, 为电极的等效屏蔽长度, 为电极的等效屏蔽长度, 表示表面电极层完全对铁电材料表面电荷进行补偿, 表示表面电极层完全对铁电材料表面电荷进行补偿, 表示为完全的介电电学边界, 表示为完全的介电电学边界, 为铁电薄膜的介电系数。 为铁电薄膜的介电系数。
在基体上制备外延铁电薄膜时,由于薄膜材料与基体材料晶格不匹配,会在薄膜内部产生残余应变 (或称错配应变),其中 (或称错配应变),其中 分别表示基体和薄膜的晶格常数。制备过程中,当薄膜厚度增加时,残余应变产生的高应变能将通过界面生成分布位错来释放,因此薄膜内部的真实残余应变将减小[12]。此时分析铁电薄膜性能的尺寸效应时,必须考虑真实的错配应变值,特别是对大于10nm的铁电薄膜尤其重要。在考虑界面位错松弛应变效应时,薄膜内真实平面内应力可表示为 分别表示基体和薄膜的晶格常数。制备过程中,当薄膜厚度增加时,残余应变产生的高应变能将通过界面生成分布位错来释放,因此薄膜内部的真实残余应变将减小[12]。此时分析铁电薄膜性能的尺寸效应时,必须考虑真实的错配应变值,特别是对大于10nm的铁电薄膜尤其重要。在考虑界面位错松弛应变效应时,薄膜内真实平面内应力可表示为
1/2 1 2 下一页 尾页 |


